算法性能分析
算法性能分析
求x的n次方
时间复杂度尽可能小。
1 | int function4(int x, int n) { |
求斐波那契数列
需要优化。
1 | // 版本二 |
解释:
- 当n<=0,返回0(因为没有数)
- 当n<3,返回1(因为前两项都是1)
- 当n==3,返回first+second(因为等于前两项相加)
- 当n>3,每次相加之后,新的一项等于前两项相加。而second表示新的一项(相当于往右移了一位)
递归算法空间复杂度的计算
递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度
因为每次递归所需的空间都被压到调用栈里(这是内存管理里面的数据结构,和算法里的栈原理是一样的),一次递归结束,这个栈就是就是把本次递归的数据弹出去。所以这个栈最大的长度就是递归的深度。
二分递归的性能分析
1 | int binary_search( int arr[], int l, int r, int x) { |
时间复杂度显然是\(O(logn)\)
每次递归的空间复杂度可以看出主要就是参数里传入的这个arr数组,但需要注意的是在C/C++中函数传递数组参数,不是整个数组拷贝一份传入函数而是传入的数组首元素地址。
也就是说每一层递归都是公用一块数组地址空间的,所以 每次递归的空间复杂度是常数即:O(1)。
再来看递归的深度,二分查找的递归深度是logn ,递归深度就是调用栈的长度,那么这段代码的空间复杂度为 1 * logn = O(logn)。
代码的内存消耗
C/C++
程序运行时所需的内存空间分为固定部分和可变部分。
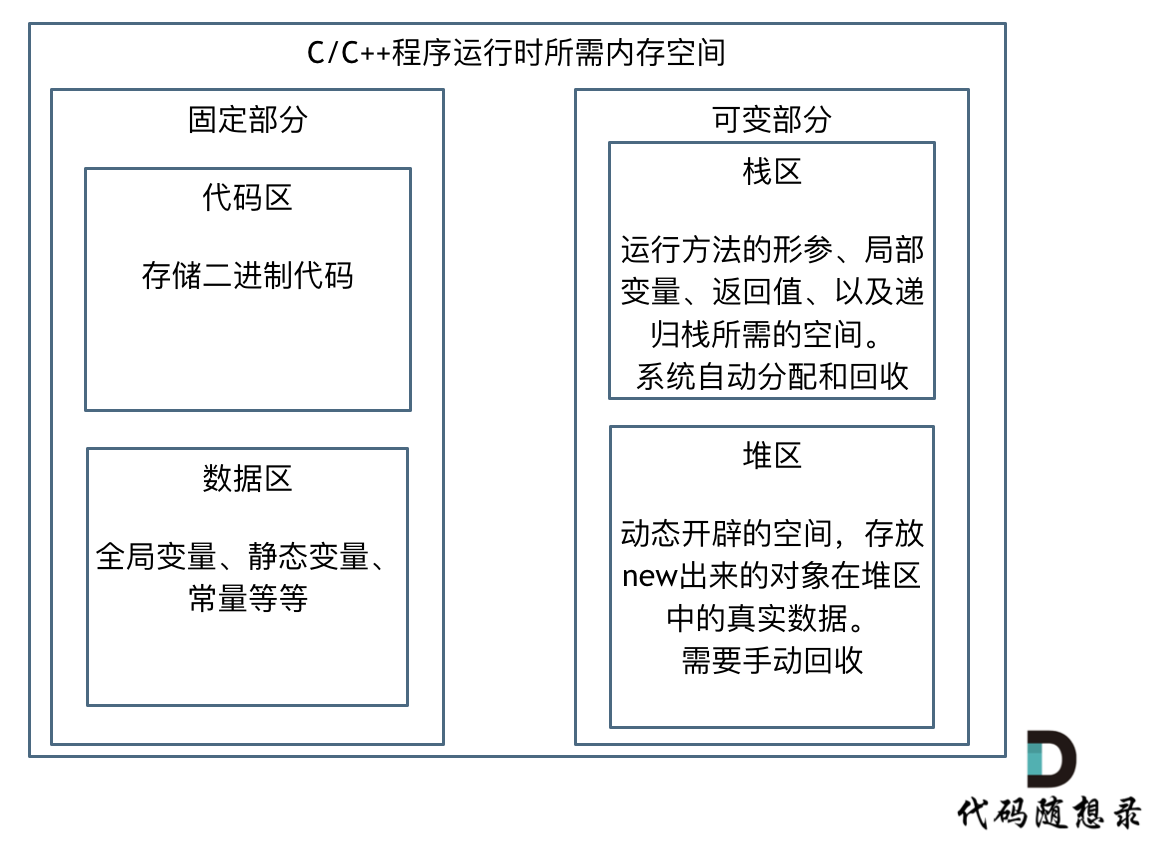
代码区和数据区所占空间是固定的,并且非常小。则运行时消耗的内存主要看可变部分。
对于可变部分,栈区间的数据在代码块执行结束之后,系统会自动回收。
而堆区间数据需要程序员自己回收,所以也是造成内存泄漏的发源地。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Torch's blog!



