密码学学习
绪论
Introduction
Course Overview

安全通信:
- 网页流量使用HTTPS协议保护(SSL)
- 无线流量:
- 比如WI-FI使用WPA2保护 ,WPA2是802.11i的一部分
- 手机流量使用GSM加密机制保护
- 蓝牙流量也可以使用密码学保护
加密硬盘的文件:
- EFS(Encrypting File System)
- TrueCrypt
保护内容:
- DVD和蓝光碟,上面的电影是加密的
- DVD用的是CSS(Content Scramble System,内容混淆系统)
- 蓝光碟用的是AACS(Advanced Access Content System,高级访问内容系统)
用户认证

HTTPS是HTTP协议的安全版本,它通过在HTTP下层使用SSL/TLS来加密数据传输。
在SSL(Secure Socket Layer,安全套接字层)更新到3.0时,IETF对SSL3.0进行了标准化,并添加了少数机制,标准化后的IETF更名为TLS1.0(Transport Layer Security,安全传输层协议),可以说TLS就是SSL的新版本3.1。也可以将TLS看作SSL的升级版
总结来说,SSL是TLS的前身,而HTTPS是使用SSL/TLS来加密HTTP通信的协议。随着网络安全的发展,TLS已经取代了SSL,并成为保护网络通信的主要安全协议。

握手协议(公钥加密)
记录层
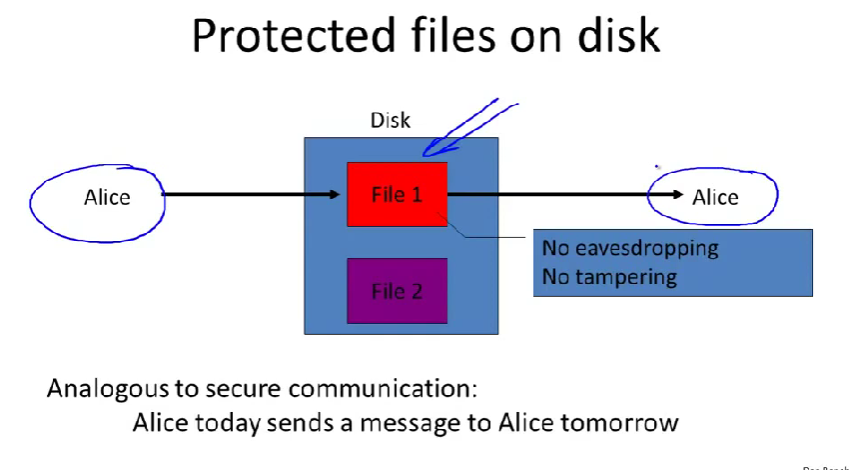
no eavesdropping——无窃听
no tampering——无篡改
analogous——类似的

sym.encryption(symmetric encryption):对称加密
cipher:指用于加解密的「密码算法」,有时也被直接翻译成「密码」
plaintext:明文
ciphertext:密文
proprietary cipher:私有加密算法(对应公开的加密算法)

一次性密钥:加密电子邮件时,通常不同邮件使用不同秘钥加密
多次密钥:加密文件时,同一密钥用来加密很多不同文件。需要更多机制保证加密系统是安全的。

密码学不能解决
- software bugs:软件bugs
- social attack:社会工程学攻击
Reliable unless implemented and used properly:除非正确实施和使用,否则不可靠
- 举例:老的加密标准WEP(加密WIFI流量)
broken:有缺陷的,不完善的
ad-hoc:临时的
What is cryptography?
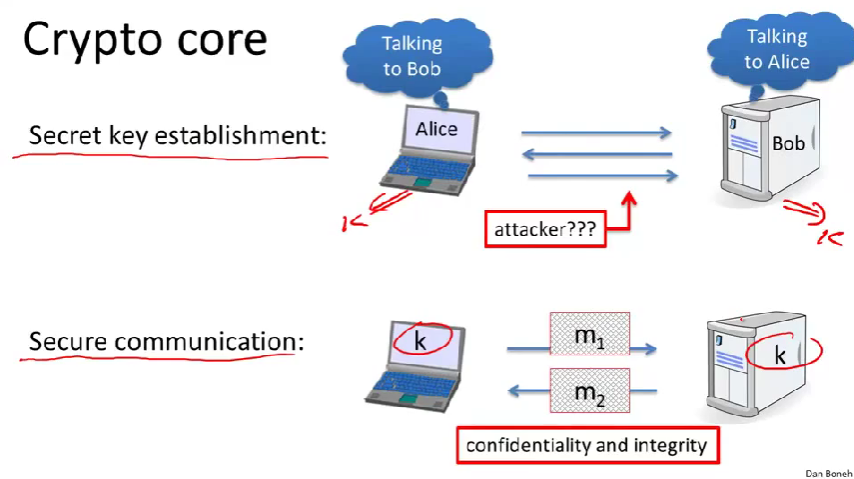
encryption schemes provide both confidentiality and integrity.(加密机制、保密性和完整性)
Cryptography Applications
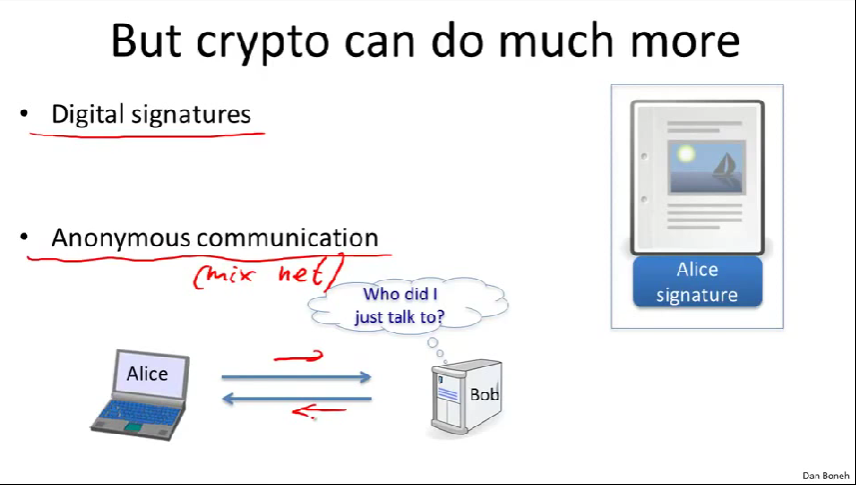
Digital signatures:数字签名
Anonymous communication:匿名通信

Anonymous digital cash:匿名数字现金
double spending:是数字货币和加密货币领域中的一个术语,指的是同一笔数字货币被花费两次或多次的情况。
一种可行的方法:making sure that if Alice spends the coin once then no one knows who she is. but if she spends the coin more than once, all of a sudden, her identity is completely exposed.
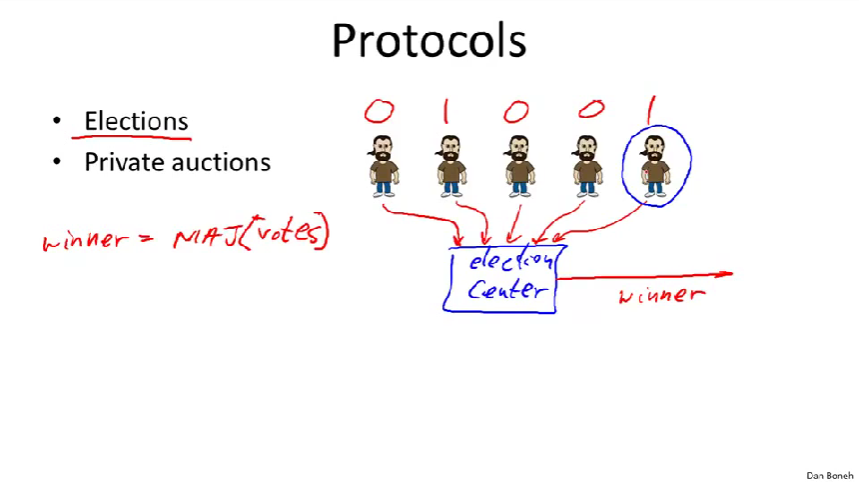
Election(选举)
- 问题:计算出多数投票结果,不过却不用知道每个人的投票结果
- 解决:引入一个election center,用来计算大多数票,不过保密投票结果,各派将他们的投票加密后送给选举中心,投票结束后,election center计算出胜者,election center还需验证投票者是否能投票以及只能投一次。
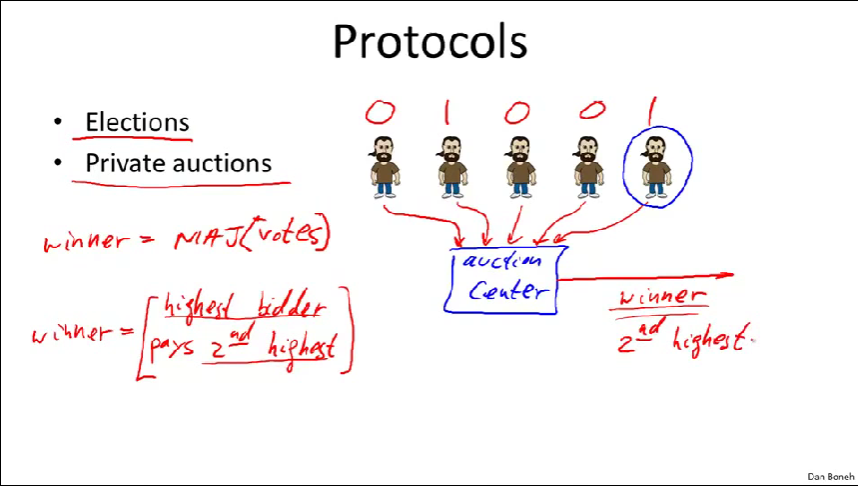
private auctions(私密拍卖)
- 问题:让参与者能计算最高出价者以及他该付的金额,除了这些,其他关于个人投票信息保密
- 解决:最高出价数额保密,为公众所知的只有第二高价的数额和最高出价者是谁。
扩展:Vickrey拍卖是指所有竞拍者通过密封投标的方式竞价,出价最高的竞拍者获得拍品,并支付第二高的报价。
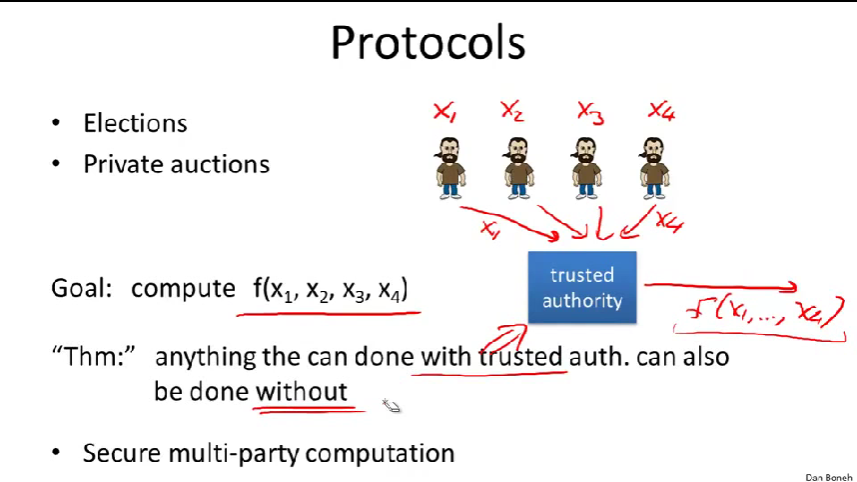
引出更广泛的问题:secure multi-party computation(安全多方计算)
如前面的election center、auction center相当于trusted authority
密码学一个核心的定理:一个任何你想做的计算,只要你能用可信任方计算,你也一定可以不借助可信任方完成。
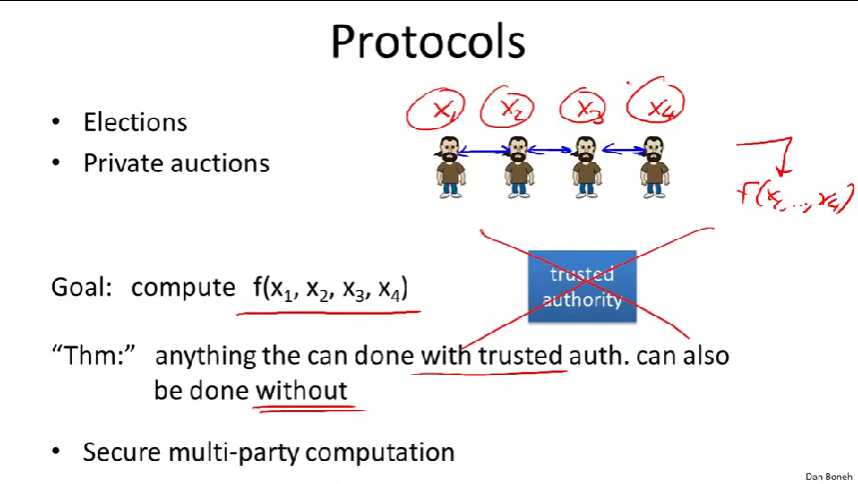
去掉可信任方,取而代之,各参与者使用某些协议互相通信。(个人信息依然保密,且没有可信任方)
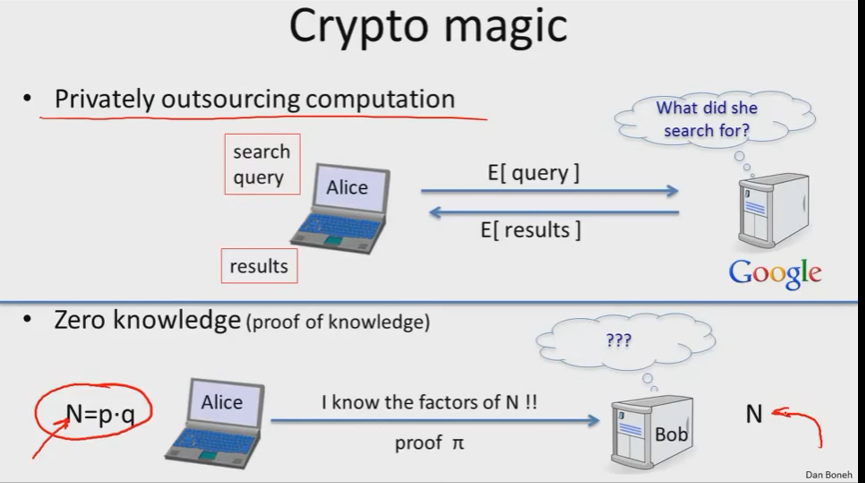
privately outsourcing computation(私有外包计算)
用户搜索请求加密后交给Google,Google扎起加密的请求上运行庞大的搜索算法,然后将加密后的结果给用户,用户进行解密后就会得到搜索结果了。(整个过程中,Google只看到了请求加密的方式,却不知道用户搜索的内容,用户得到了搜索的结果)
zero knowledge(proof of knowledge)零知识证明
数N为两个大质数p和q的积,现给出N,求质数分解结果。
零知识证明的神奇之处:Alic能向Bob证明她知道N的因子分解,这个证明能给Bob,Bob检查后确信Alice知道如何分解,但是Bob不知道因子P和Q。(举例子理解,你解出了一个数独谜题,你可以将其给Bob,Bob可以证明你解决了,但不知道你是怎么解出来的)

rigorous:严格的
forge:伪造
三步(下面以数字签名为例):
- 准确描述威胁模型(比如攻击者如何攻击数字签名,伪造签名目的何在)
- 提出架构
- 证明任何攻击者在这个威胁模型下可以攻击这个架构的,这个攻击者也可以用来解决根本性难题。(如果问题很难,实际上就证明了攻击者无法在威胁模型下,破解这个架构)
Symmetric Encryption
History
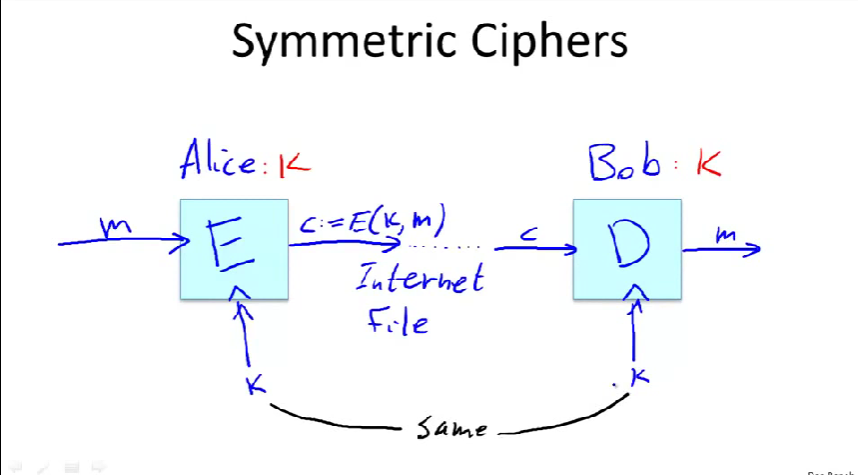
图中老师使用符号的意义:
->>表示密钥输入
:=定义变量C代表了什么

替换加密
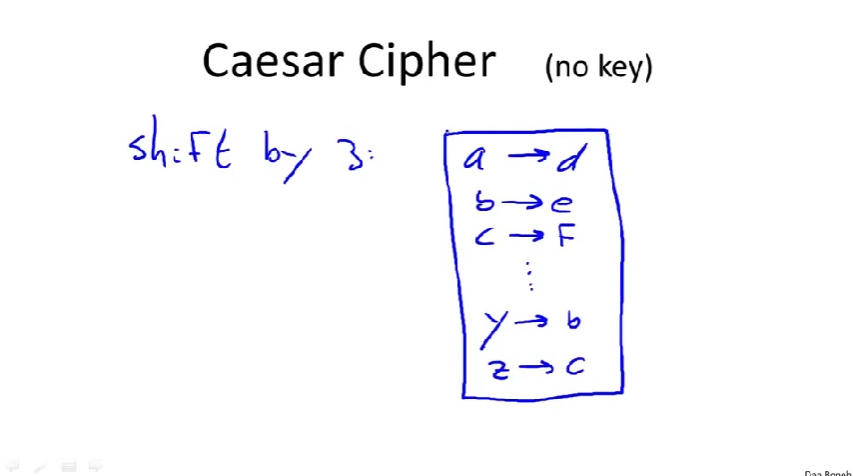
替换加密的一个例子:凯撒密码
字母移动三位,可以说它不是cipher,因为没有密钥,或者说密钥固定。

替换加密的密钥空间是26!,约为\(2^{88}\)
密钥空间(Key Space)是密码学中的一个概念,指的是在特定加密算法中所有可能密钥的集合。(密钥空间是所有可能的密钥组成的集合,每个密钥都是该空间中的一个元素。)
密钥空间的大小通常由密钥的位数和可能的字符(通常是2的幂)决定。例如,一个8位的密钥空间大小为\(2^8\)个可能的密钥。

破解替换加密:
- 字母的频率
- 字母配对的频率
替换加密对于唯密文攻击是脆弱的。
唯密文攻击:仅对截获的密文进行分析,求解明文或密钥的密码分析方法。
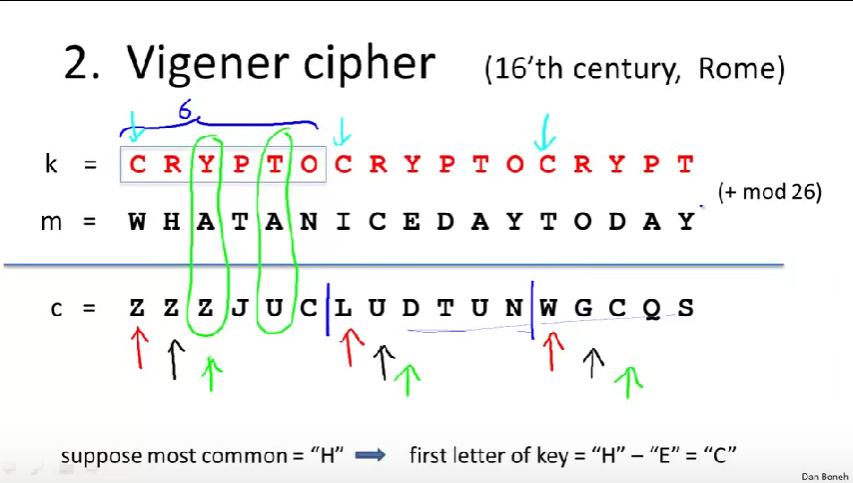
步骤:
- 先将密钥重复写,以至于每个明文都能对应一个密钥的字母,如图中的k=CRYPTO,重复写。
- 然后将明文字母和密钥字母相加模26得到密文
- 解密:重复写密钥,密文减去密钥
破解Vigener cipher:
- 分组,每组的同一个位置用的是同一个密钥字母加密
- 观察每组该位置出现最频繁的密文字母,则很可能其是E加密过来的(如图中的假设是H,则H-E=C,C则是密钥的一个字母)
- 继续找下一个位置,如上述步骤找的是第一个,后面接着继续,直到将密钥完整破解出
- 以上的步骤是基于知道密钥长度的情况下,如果不知道密钥长度,可以先假设密钥长度是1,开始解密,接着假设为2,解密......直到得到一个说得通的信息。

rotor machines:转轮机
输入一个字母,碟片旋转。如图中,输入三次C,分别是T、S、K。
该机器一经提出,很快就被破解,使用字母频率、配对频率、三合字母频率。(唯密文攻击)


DES(Data Encryption Standard):密钥空间\(2^{56}\)
Discrete Probability
finite set:有限集
全局U上的概率分布为一函数记为P,该函数为全局中的每一个元素赋值,范围在0到1之间,这个数称为全局中特定元素的权重或概率。所有权重和为1。

uniform distribution:均匀分布

point distribution:点分布
将所有权重放在一个点上。
distribution vector:分布向量

每个字符串的概率符合均匀分布。
\(lsb_2(x)=11\),x的低两位是11

the union bound:并集上界
\(msb_2(x)=11\),x的开头两位是11
使用并集上界来估算概率的上界。

Random Variables:随机变量

the uniform random variable:均匀随机变量

\(r_1\)和\(r_2\)是r的第一位和第二位
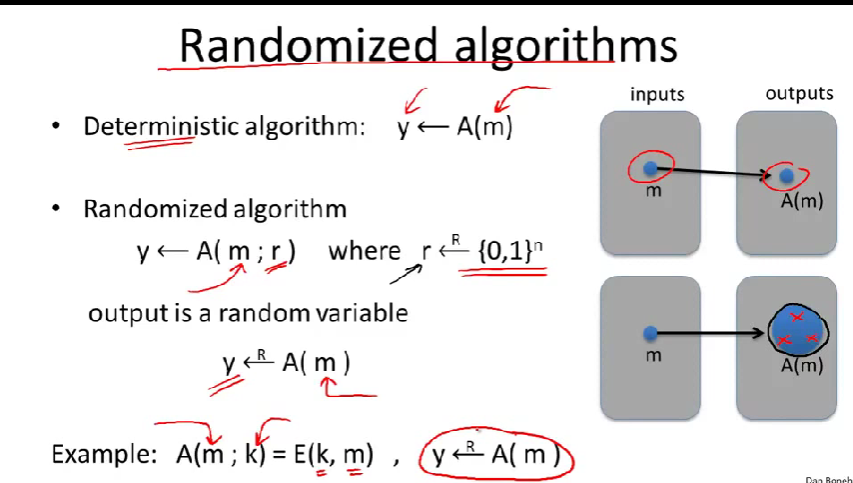
Deterministic algorithm:确定算法
不同的输入,输出总是一致的。

independence:独立性

the XOR is basically just the addition modular two.(模2和)

随机变量Y随机分布于\(\{0,1\}^n\),另一独立的随机变量X在\(\{0,1\}^n\)上均匀分布。随机变量Z为X和Y的异或和,不管Y怎么分布,Z总是均匀分布的随机变量。
证明\(n = 1\)的情况。

the birthday paradox:生日悖论
从全局U中选择n个随机变量,这些随机变量是相互独立的,它们不一定是均匀分布的,只需假设它们同分布。
两次取样相等的概率\(\ge \frac{1}{2}\)。
流密码
The One Time Pad

a cipher is defined:
key space:the set of all possible keys
the set of all possible messages(明文)
the set of all possible ciphertexts

the one time pad:一次性密码本
密钥空间和明文空间和密文空间是一样的
密钥、明文、密文等长。

加密解密原理的证明

密钥要和明文一样长,而且是一次性的,这就导致了Alice和Bob要安全通信,Alice要发送一条消息给Bob,在她发送信息的第一位之前,她需要给Bob传送一个密钥。如果她有办法安全地传送给Bob一个密钥,她就可以用这个办法直接传送明文了(密钥和明文一样长)。

perfect secrecy的定义
where k is uniform \(\mathcal{K}\):密钥是均匀分布在密钥空间上(老师的符号表示:\(k\overset{r}\leftarrow\mathcal{K}\),k是均匀分布在密钥空间上的随机变量)
意思:如果我是攻击者,我截获了一段密文c,密文是\(m_0\)的加密结果和是\(m_1\)的加密结果的概率相等。
对于具有perfect secrecy(完美安全)的密码,任何唯密文攻击无效。

对于任意给定的密文,其加密成明文c的密钥数量是常量,又因为分母是密钥空间数量,所以概率相等。(这样更好理解点)参考

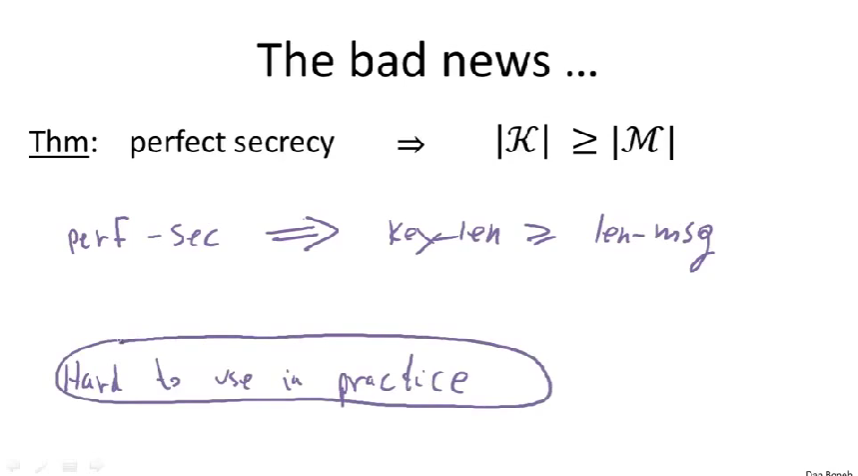
Stream ciphers

PRG(pseudo-random generator):伪随机发生器
PRG is a func(图中用G符号表示)
这个函数取一个种子(\(\{0,1\}^s\)为seed space,种子空间)作为输入,它将一个s位的种子映射到长得多的字符串(图中为n位)
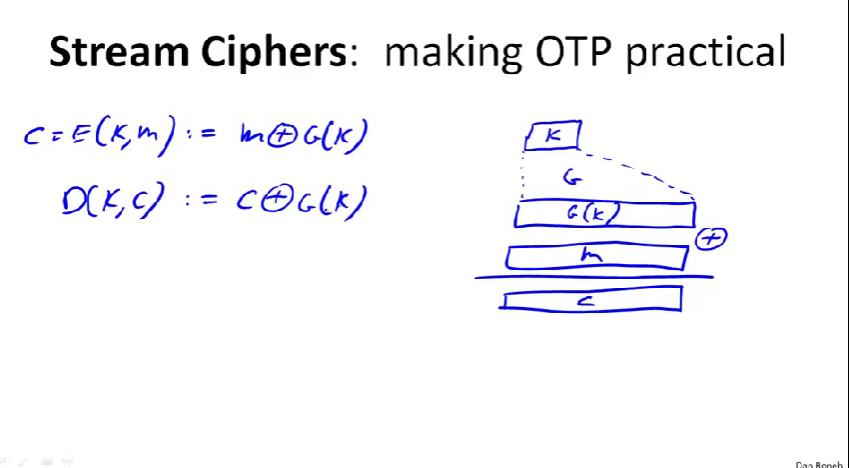
用种子作为密钥,使用发生器将其扩展成长得多看起来很随机的序列,或称为伪随机序列。(即图中G(K))然后进行异或操作。

流密码中是完美安全的吗?
不是,因为密钥长度远远小于明文长度。

unpredictable:不可预测性
定理:存在一个数i,如果我们给出PRG输出的前i位,存在某种有效的算法,可以计算余下的字符串。如果是这种情况,那么这个流密码是不安全的。
因为基于一些预知的知识,攻击者知道信息的某些部分最初的明文内容
- 例子:因特网电子邮件标准协议之一的SMTP,这个协议的每条信息都以from:开头,那是攻击者预先知道的前缀,所以攻击者可以将from:的密文与事先预知的明文异或,这样就得到了伪随机序列的前缀。
- 由于该例子是基于如果一个流密码是可预测的(PRG可预测),则可以预测到伪随机序列的剩余部分,也可以预测到明文的额剩余部分。
- even:能预测一位也会造成问题,因为依次预测下去,就相当于都能预测。

存在一个有效算法A,还有一个位置i(位于0到n-1之间)
\(k\overset{r}\leftarrow\mathcal{K}\):表示从\(\mathcal{k}\)这个密钥空间随机选取一个密钥k。
Pr[]:表示概率。
将G(k)输出的前缀(这里给前i位 )输入给算法A,算法能预测下一位的概率。
for some non-negligible, denote them as \(\epsilon\).对于一些不可忽略的量,用\(\epsilon\)表示。
\(\frac{1}{2}\):下一位要么是0要么是1,所以预测准确的概率是\(\frac{1}{2}\),如果再加上一个不忽略的量\(\epsilon\),就表示大于\(\frac{1}{2}\)。
(最下面的定义:通俗的来讲就是不管给什么样的前缀,也无法预测出前缀的下一位。)
例子:
(1)

\(XOR(G(k))=1\):所有位异或为1。
是可预测的,因为如果给了前n-1位,可以预测第n位。不满足任意i的定义。
(2)

linear congruential generator:线性同余生成器
it has three parameters:a,b,p.(a和b是整数,p是质数)
以\(r[0]\)为生成器的种子,然后迭代运算下面的式子。
\(r[i] \leftarrow (a\cdot r[i-1]+b )\ mod \ p\)
然后输出几位关于目前状态i的数\(r[i]\),然后i+1
这个生成器具有良好的统计学性质,很容易被预测。
glibc:GNU C Library函数库

the definition of Negligible and non-negligible
- 实用派
- 密码学理论
实用派认为,如果一个值比\(\frac{1}{2^{30}}\)(约为十亿分之一)大,那么就不可忽略的。(原因是你用密钥加密一个G的数据,约为\(2^{30}\)字节,\(2^{33}\)位,那么\(\frac{1}{2^{30}}\)概率的事件就会很有可能发生。)反之,当一个值小于\(\frac{1}{2^{80}}\),那么就是忽略的。
函数值大于1除以某个多项式的值,则说是不可忽略的。如果函数值小于1除以所有多项式对应的值,就说它是可忽略的。
(\(\lambda_d\)可以理解为,对于\(\forall d\),与其对应的下界)
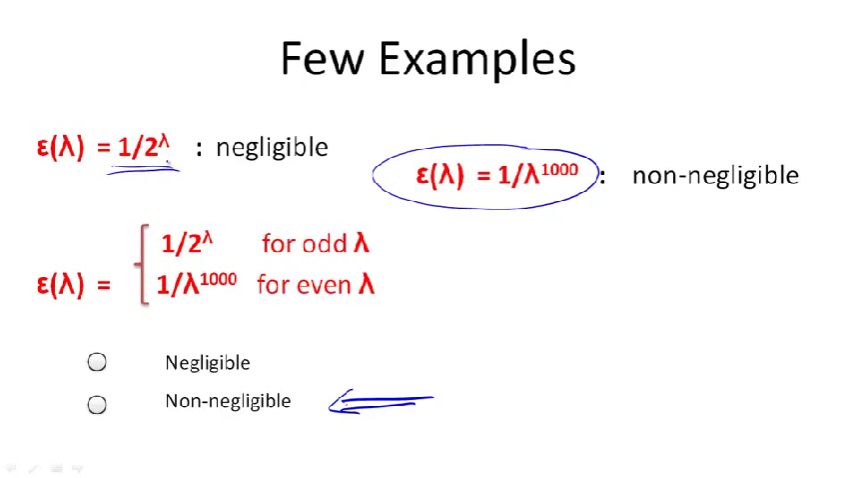
例子
\(\epsilon(\lambda)=\frac{1}{2^\lambda}\)
- 对于\(\forall d\),总存在一个足够大的\(\lambda\)满足\(\frac{1}{2^\lambda}<\frac{1}{\lambda^d}\)。一个是指数级别的,一个是幂指数。
\(\epsilon(\lambda)=\frac{1}{\lambda^{1000}}\)
- 显然,如果d取10000,\(\frac{1}{\lambda^{1000}}>\frac{1}{\lambda^{10000}}\)。
\(\epsilon(\lambda)=\begin{cases}\frac{1}{2^\lambda} & \text{for odd } \lambda,\\\frac{1}{\lambda^{1000}} & \text{for even }\lambda\end{cases}\)
- 满足non-negligible的定义
Attacks on OTP and stream ciphers
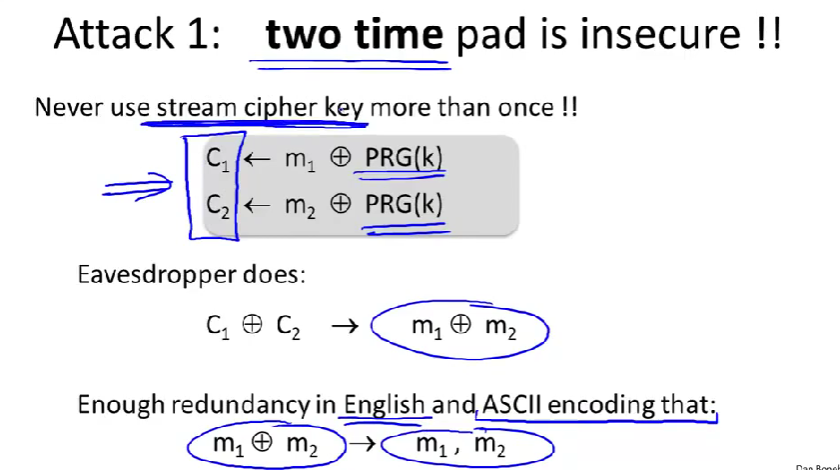
two time pad attack:两次密码本攻击
一次性密码本之所以叫一次是因为密码本只能加密单个信息。接下来将展示,如果同样的密码本为不同的明文加密,就不再安全。
eavesdropper:窃听者
密文\(C_1\)与\(C_2\)异或等价于\(m_1\)与\(m_2\)异或,因为密码本被异或抵消了。
Enough redundancy in English and ASCII encoding that:英语实际上有者足够的冗余(如某些字符出现频率高,某些低),用ASCII码编码,本身就有足够的冗余了(ASCII码中有很多用不上的,控制字符)

Project Venona:苏联靠人工掷骰子生成密码本,由于生成密码本颇费人工,用来加密一条信息显得浪费,所以最后用来加密多条信息。美国最后仅凭截获密文破解了。
MS-PPTP(point-to-point tunneling protocol):它是关于客户端希望与服务端安全通信的。客户端与服务端共享一个密钥。将双方的整个互动当做一个流
图中双竖线代表联结,本质上将客户端和服务端的信息全部联结成一个长流。整个长流用流密钥K来加密。服务端也在发送同样的事(也是使用流密钥K)。所以发生的与二次密码本别无二致。
- 解决:可以用两个密钥,一个是服务端到客户端,一个是客户端到服务端,双方都保有这对密钥。
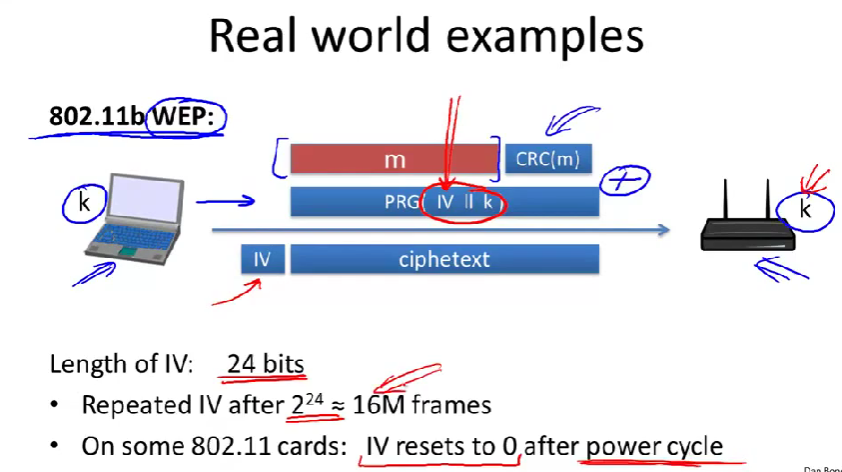
图中有一个客户端和一个接入点,它们共享一个密钥k。
比如客户端想发送一个包含明文m的帧给接入点,CRC(m)是校验和。明文m和校验和要用流密钥加密。(这里的流密钥是一个值IV(为24位字符串,从0开始取值,可以是一个数据包的计数器,这样每个数据报的IV不同,于是每个数据包的IV加一)和一个长期的密钥K的联结)
problem:IV是24位,也就只有\(2^{24}\)个,经过1600万帧的传输后,IV又要从0开始了。于是就有了二次密码本。
on some 802.11cards:IV resets to 0 after power cycle.:在一些802.11的网卡上,在重启系统后,IV会重置为0。(所以会造成同样的密码本用来加密许多不同的信息)
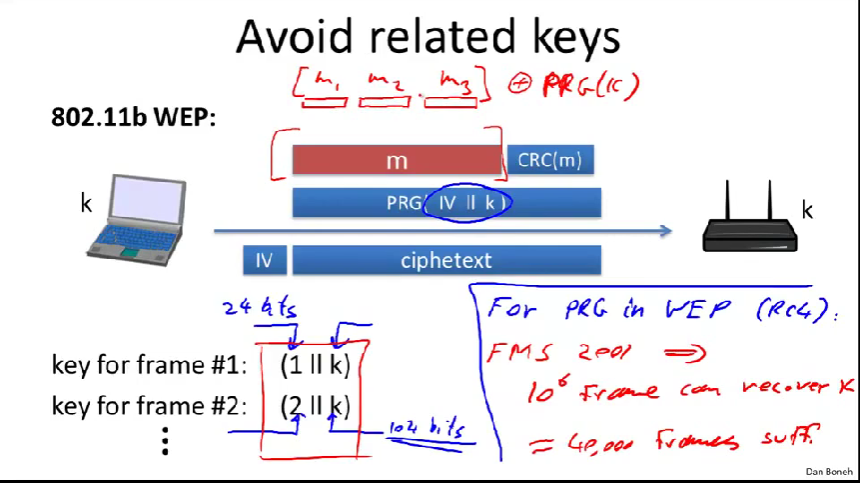
第一帧的密钥是1和k的联结,第二帧是2和k的联结,以此类推。
k是104位,所以PRG生成密钥是104+24=128位。
它们的后缀104位都是一样的,大部分密钥都是相近的。
WEP中使用的PRG叫做RC4,FMS(三个人,Fluhrer,Mantin,Shamir)于2001年发现,证实经过\(10^6\),约一百万帧后,就可以还原密钥了。
办法:
- 1.对帧进行处理, 将所有客户端发向服务端的帧当做一个长流处理,对长流使用伪随机数发生器(PRG)来进行异或操作。(比如密码本的第一节用来加密M1,密码本的第二节用来加密M2,以此类推)
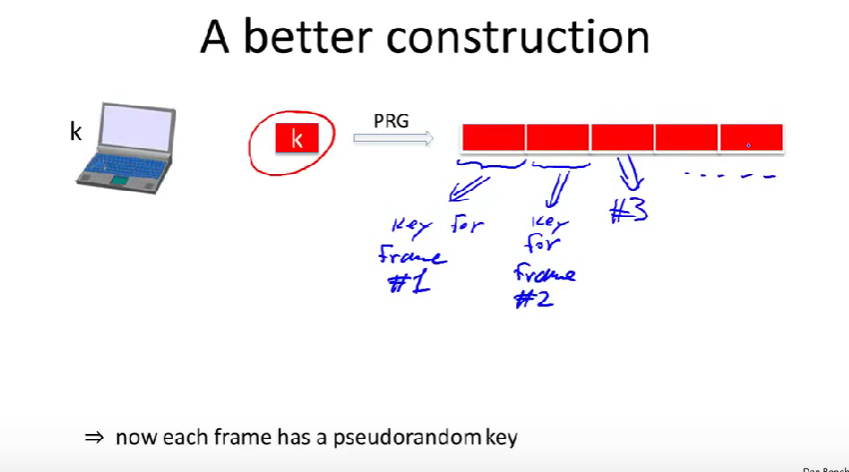
- 2.再次使用PRG,获得一个长期密钥,然后把密钥输入给PRG,得到一个长流。(可以用第一段来加密第一帧,第二段加密第二帧,以此类推。)
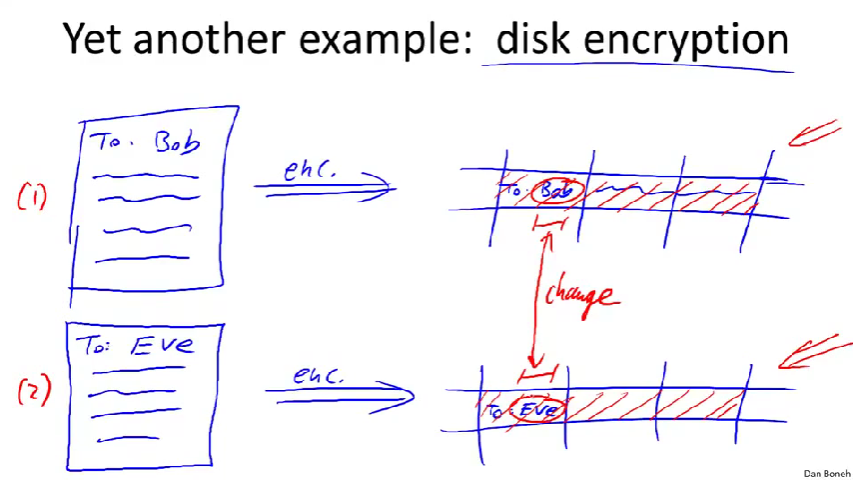
disk enccryption:硬盘加密
老师用红色的斜线表示这被加密了。
原始文件是(1),过一段时间后,用户修改了文件,现在不是给Bob了,而是要给Eve了,但文件其余内容不变。攻击者查看了修改前硬盘的内容,现在又来查看修改后硬盘的内容。他会发现改变的仅仅是一小段不一样了,其他都是一模一样的。
所以在硬盘上使用流密码加密是不明智的,本质上是二次密码本攻击的又一个例子,相同的密码本被用来加密两条不同大的信息。
总结
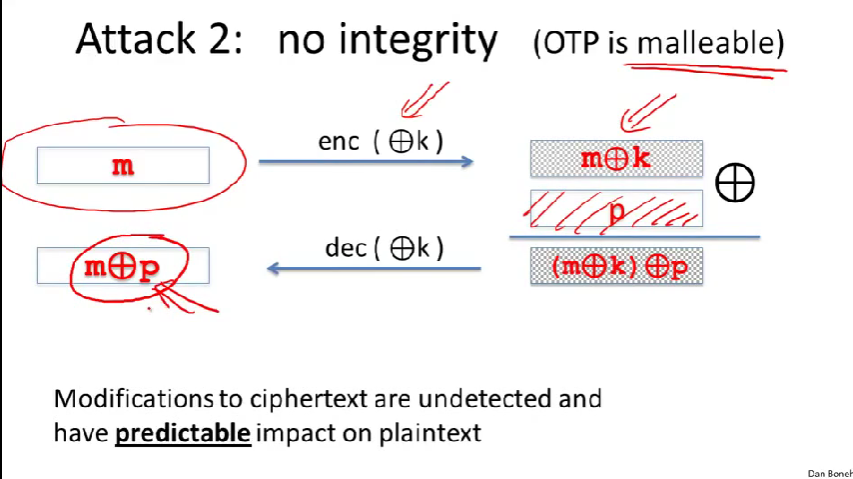
一次性密码本和流密码不提供完整性保护,只提供私密性保护。
malleable:在密码学中,"malleable"(可塑的或可变形的)这个术语通常与某些加密算法的弱点有关,特别是那些允许攻击者在某种程度上修改密文,从而影响解密结果的算法。这种类型的攻击被称为"可塑性攻击"(malleability attack)。
假设攻击者将密文与一特定值P异或,P叫做子置换密钥。
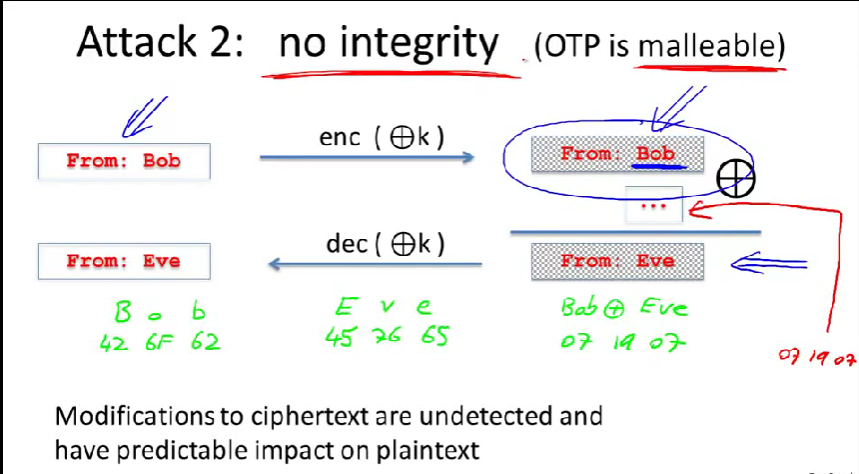
攻击者想修改这封信,让它来自于另外某个人(比如Eve),他可以用异或特定的三个字母。(前提假设是他知道这信来自Bob,以及知道在密文正确位置异或这三个字母。)
将Bob和Eve进行异或(ASCII),得到07 19 07。
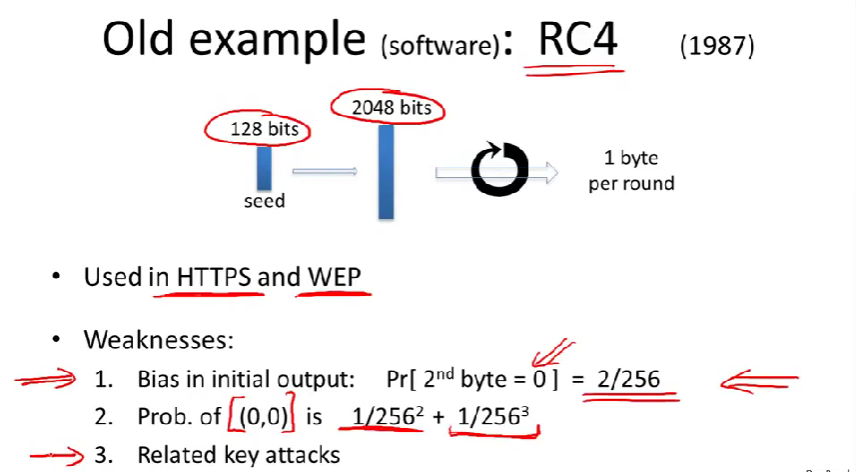
RC4种子大小可变,例如可以是128位的,它将被用作流密码的密钥。
步骤:
- 将128位的密钥扩展导2048位
- 执行一个非常简单的循环,每一轮输出一个字节。
Weaknesses:
Bias in initial output: \(Pr[2^{nd}byte=0]=\frac{2}{256}\)
- 第二个字节有点不均匀。
- 如果是完全随机的,第二个字节为0的概率应该是\(\frac{1}{256}\)。(也就是说如果用来加密一段信息,第二个字节就更有可能不会被加密,换句话说,它比正常多一倍的概率和0异或。)
- 事实上,第一个字节和第三个字节也是不均匀的。
- 解决:RC4-drop,忽略发生器的前256个字节,从发生器产生的第257个字节开始。(前面的字节是不均匀的)
Prob.of (0,0) is \(\frac{1}{256^{2}} + \frac{1}{256^{3}}\)
- 如果看RC4一段很长的输出,会发现出现序列00的可能性更大。
- 如果是完全随机的,那么出现序列00的可能性是\(\frac{1}{256^{2}}\)
Related key attacks
- 使用的密钥之间紧密联系,实际上是可能还原根密钥的
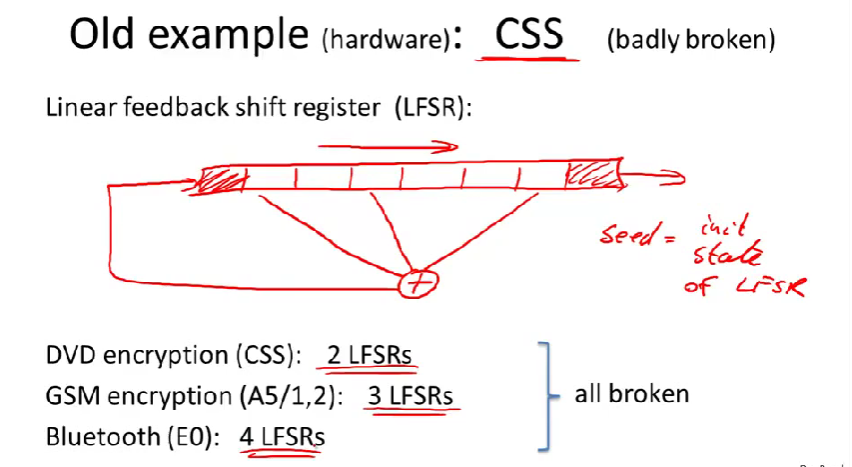
CSS(content scrambling system):内容混淆系统
用于加密DVD电影的
它是基于线性反馈移位寄存器(LFSR)设计的。
- LFSR是由若干单元组成的寄存器,每个单元含有一位。(特定的单元有出头,不是全部单元都有)这些出头被异或。
- 在每一个时钟周期,寄存器向右移一位。(最右位被丢弃,而异或结果被当做第一位)
- LSFR的种子就是寄存器的初始状态。
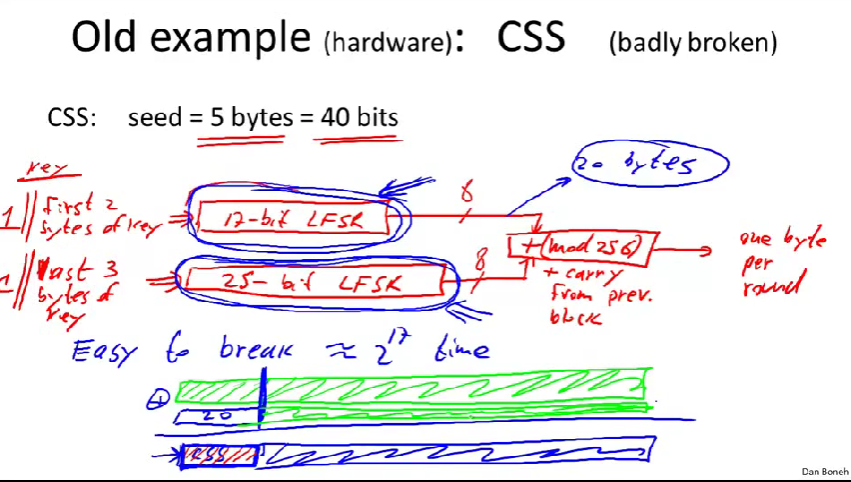
CSS的密钥是5个字节,40位。
- 40位的原因:是因为涉及DVD加密算法时,美国出口法规定,出口的加密算法密钥只能是40位。
CSS使用两个LSFR,一个数17位LFSR,另一个是25位LFSR。(也就是说一个寄存器含17位,另一个为25位)
种子生成的方式:第一个17位寄存器的初始状态是:开头是1,然后联结密钥的前两个字节。(刚好是17)另一个寄存器:1联结上密钥大的后三个字节。(刚好是25)(总共用了5个字节,恰好使用了密钥的长度)
一轮输出一个字节,然后这个字节和DVD数据里面的字节进行异或加密。
破解:
- 由于DVD加密使用的MPEG文件,如果你知道明文的前缀(比如前20个字节),然后异或明文前缀与密文,就能得到PRG最初输出(即CSS输出的前20个字节)的分段。
- 对于\(2^{17}\)的一种猜测,运行第一个LSFR生成20个字节,再用PRG最初输出(CSS输出的前20个字节)减去第一股LSFR输出的20个字节。
- 如果猜测对的话,得到应该是第二个寄存器的前20字节的输出。
- 判断:实际上看20字节序列,很容易判断这20个字节是否来之一个25位LSFR的输出。如果不是,证明对17位寄存器的猜测错误。
- 最后一直尝试,不仅能得到17位寄存器的初始状态,也能得到25位寄存器的初始状态。
- 然后就能解密出CSS的剩余输出,从而能解密整个电影了。

输出长度是远大于输入的。
Nonce:在密码学中,Nonce是一个缩写词,它代表"Number used once"或"Number once"。Nonce是一个随机或伪随机生成的值,用于确保加密的唯一性,防止重放攻击(replay attacks)和其他类型的攻击。
the nonce makes the pair(指的是(k,r)有序对) unique.
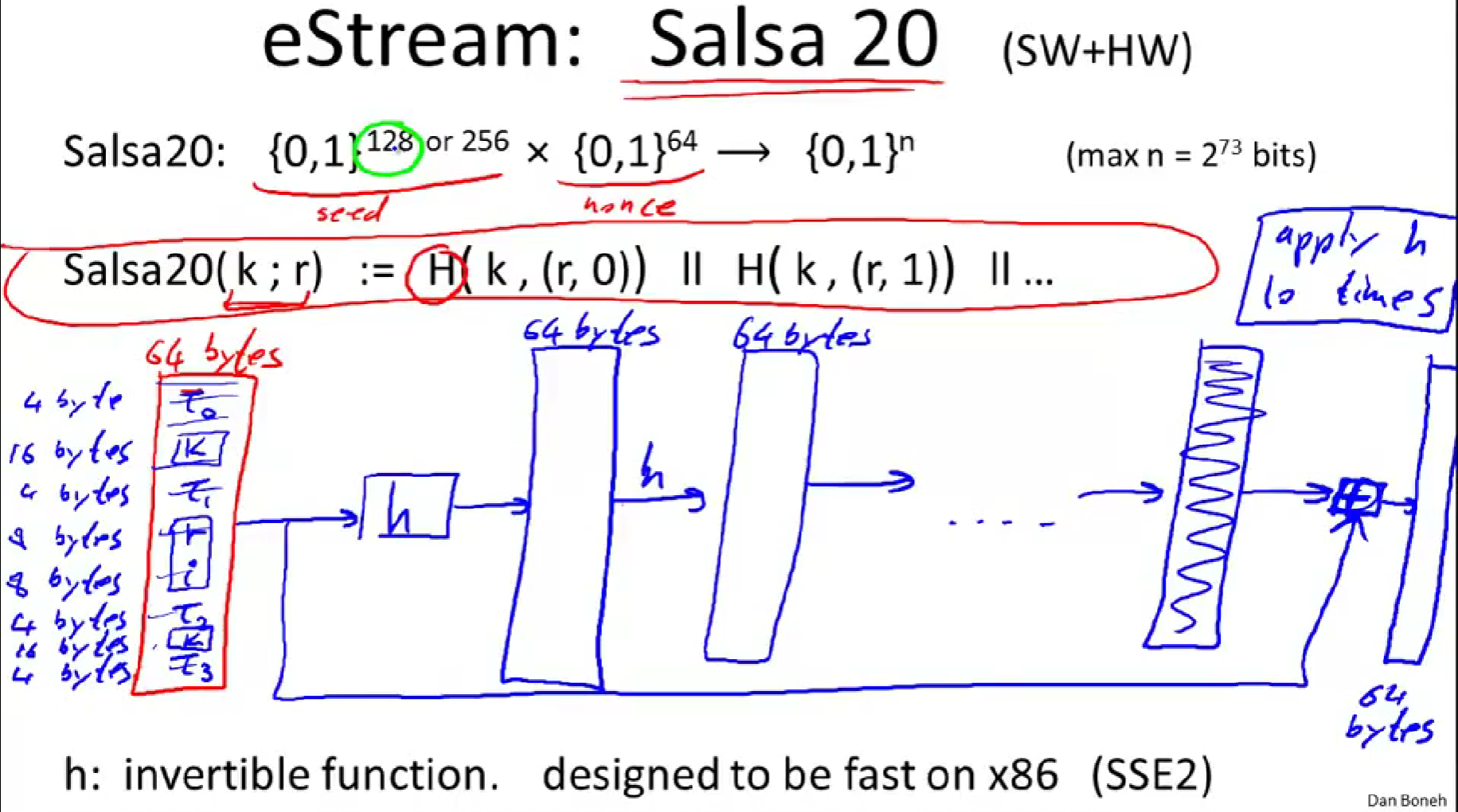
Salsa 20:是一个同时面向硬件和软件设计的流密码。
Salsa输入128位或256位的密钥。r是nonce。
H函数有3个输入,密钥k,nonce r,以及步骤计数器就是图中的0,1...
函数H的工作过程:
- 先把状态扩充至64字节长,定一个4字节的常数,记作\(\tau_0\)。
- 然后取16字节的密钥k,然后还要定另外一个4字节的常数,记作\(\tau_1\)。
- 然后取8字节的nonce,然后再取索引,也就是计数器,也是8字节长。
- 然后还要去另外一个4字节的常数\(\tau_2\),然后再次取密钥(16字节)。
- 最后取一个4字节的常数\(\tau_3\)。
- 以上总和就是64字节长。
- 然后应用函数h,h是一个一一对应的双射函数,由64字节映射到64字节,完全可逆。
- 然后反复应用函数h,基本上要来10次。(由于h是可逆的,从输出可以一直逆推到输入)
- 将输入和输出逐字相加(这里是64字节,4字节一次地加),最终得到64字节的输出。

2.2GHz的x86机上的性能参数。
PRG Security Defs

令PRG有密钥空间K,即N位字符串的集合。
我们的目标是定义发生器的输出和随机序列无法区分的意义。(换句话说,我们要定义一个分布,从密钥空间里选择密钥时的分布)。带R的箭头意思是从集合K里均匀地随机选取,然后发生器输出。
蓝圈代表所有N位0,1的字符串,那么均匀分布会以同等概率输出这些字符串。不过这个发生器G生成的伪随机分布,因为种子空间太小,可能输出结果的集合是很小很小的。红色区域是N位0,1字符串集合中一个很小的子集,这是发生器所能产生的一切。
- 我们说,有个攻击者在观测发生器的输出,也就是这个小集合的元素,它与均匀分布的输出无法区分。这个性质就是我们想要的。

为了理解如何定义这个与真随机不可区分的概念,我们需要引入统计测试的概念。我来定义N位0,1字符串的统计测试,我用字母A来表示这些统计测试。
统计测试是一个算法,以N位字符串为输入,输出0或1。当结果为0时,表示输入的字符串不是随机的;当结果为1时,表示输入的字符串是随机的。(所以,统计测试所做的就是取输入x,即给定的n位字符串,然后判断它是否看起来像是随机的)
例子:
- (1)对于一个随机字符串,0的个数和1的个数大体相等。(换句话说,统计测试输出1,当且仅当字符串x里0的个数减去1的个数不会差太多。比如说,0个数和1个数的差别小于\(10\sqrt{n}\))
- (2)出现连续两个0,对于一个随机字符串,我们期望00的概率应该是\(\frac{1}{4}\),对于一个随机字符串,我们期望大于有\(\frac{n}{4}\)个00。

- (3)我们说统计测试输出1,当且仅当最大的块,我们叫0的最大游程,在字符串x中最长的连续的0。在随机字符串里,我们有一个期望0的最长游程,如果小于则是随机的,如果远远大于,则是不随机的。(对于全1的字符串,这个统计测试也会认为是随机的,因为符合,所以说,统计测试不一定是对的。)

在我们讨论安全性定义前,我们还需讨论如何评估一个统计测试。为此,我们定义优势的概念。 \[ ADV_{PRG}[A,G]=|Pr_{k\overset{R}\leftarrow\mathcal{K}}[A(G(k))=1]=Pr_{r\overset{R}\leftarrow{\{0,1\}^n}}[A(r)=1]|\le[0,1] \] 我们有一个生成N位字符串的发生器,有N位字符串的统计测试。统计测试A相对于发生器G的优势,定义为两个量的差,第一个量是统计测试输出1的可能性(当输入是由发生器生成的伪随机输出),同时我们还要看输入是真随机字符串时输出1的可能性。两个量的差(由于是概率的差,差的区间在[0,1]里)
我们定义这个发生器的优势,记为优势子PRG。
讨论:
- 如果这个优势接近于1,意味着我们输入伪随机数和输入真随机数时统计测试A表现得完全不同。(统计测试能将这个发生器的输出和真随机区分开来。从某种意义上说,这个统计测试破解了发生器G。)
- 如果这个优势跟0很近,意味着统计测试在两种情况下表现地基本一致。(这个统计测试无法区分发生器输出和真随机。 )
例子:


定义什么是安全的伪随机数发生器。
- 如果不存在有效的统计测试,可以区分发生器G的输出和真随机序列。(对所有有效的统计测试,统计测试A对发生器G的优势基本上可忽略,换句话说,它很接近于0。)
- 有效是说,测试算法总在有限步内终止并返回结果。
能否构建这么一个发生器,然后证明它是个安全的PRG,换句话说,证明没有一个有效测试能够区分发生器的输出和真随机。答案是:不能。
- 原因:如果能证明一个特定的发生器是安全的,那就意味着\(P\neq NP\)。如果\(P=NP\),那么就很容易证明不存在安全的PRG。(后句和前句是逆否命题)
- 理解:
- \(P\)是指可以在多项式时间内解决的问题,\(NP\)是指可以在多项式时间内验证解答的问题。如果\(P \neq NP\),说明有些问题在多项式时间内是无法解决的,但它们的解可以在多项式时间内验证。
- 安全的PRG:一个安全的PRG意味着它不能在多项式时间内被破解。换句话说,如果你能证明一个PRG是安全的,就说明没有多项式时间算法能够破解它。这意味着存在一些问题无法在多项式时间内解决。
- 如果\(P = NP\),所有NP问题都可以在多项式时间内解决。这意味着所有通过NP问题构建的PRG都可以在多项式时间内被破解,因为这些问题现在变得容易解决了。
P和NP问题:
- P问题相当于很容易找出一个解(比如求公约数),NP问题相当于很容易验证一个解是否正确(比如拼图)。可以看出,NP问题是包含P问题的,那么P问题是否也包含NP问题。(即P问题和NP问题是否是一回事)
- "简单"不是一个严格的数学术语,更精确的定义:所谓简单的问题,指的是能在多项式时间内找到答案的问题。如果存在一个多项式时间的算法来解拼图,那么这个问题也就属于P类。

unpredictable:给定发生器输出的前缀是不可能预测出输出的下一位是什么。
相当于必要条件一样,逆否命题:如果一个PRG是可预测的,说明它就是不安全的。

定义统计测试B:给定字符串x,B在前i位运行算法A,统计测试问算法A是否成功地预测了第i+1位,如果成功了,返回1;如果不成功,返回0。

姚期智证明了:逆命题也成立。
对任何位置i,不可能根据前i位预测输出的第i+1位,那么这个发生器就是安全的。
解读:这些下一位预测算法试图预测第i+1位,给定前i位,如果它们不能把G的输出和真随机区分开来,那么就没有统计测试可以区分G和真随机。

由题设条件,容易构造出一个统计测试来区分G的输出和均匀分布的序列,意味着G不安全-->由姚定理,得到G是可以预测的。

符号定义:
均匀分布不可区分到两个一般分布间的不可区分。
给出两个分布\(P_1\)和\(P_2\),然后问这两个分布可区分吗?
我们说这两个分布计算上不可区分,记为\(P_1\approx P_2\)
从分布\(P_1\)里取样,将结果交由A进行测试,作为对比,从\(P_2\)取样,也交给A,那么基本上A对两种情况表现一直,换句话说,两概率的差别是可以忽略的。
Semantic security
Semantic security:语义安全

- 给定密文,攻击者无法还原密钥。(当然,这是一个不好的定义。比如,想想一个聪明但失败了的密码,使用密钥k,但直接输出明文作为密文,攻击者也不能还原密钥)
- 给定密文,攻击者无法还原明文。\(M_0||M_1\)表示联结\(M_0\)和\(M_1\)。图中显然满足这一条,但是这是个不安全的定义,因为泄漏了一半的明文内容。

\(|m_0|=|m_1|\)表示两个相同长度的信息。
攻击者无法知道来自哪种分布,是加密\(M_0\)的,还是加密\(M_1\)的。
香农的完美安全定义太强了,需要很长的密钥,如果密钥太短,不可能满足这一定义。特别地,流密码不可能满足这个定义,然后,我们试图减弱这个定义,先不要求两个分布绝对相同,我们可以要求两个分布在计算上不可区分。但它还是有点太强了,无法被满足,不是说对所有的\(m_0\)和\(m_1\)满足,而是只对攻击者能想到的明文\((m_0,m_1)\)成立。
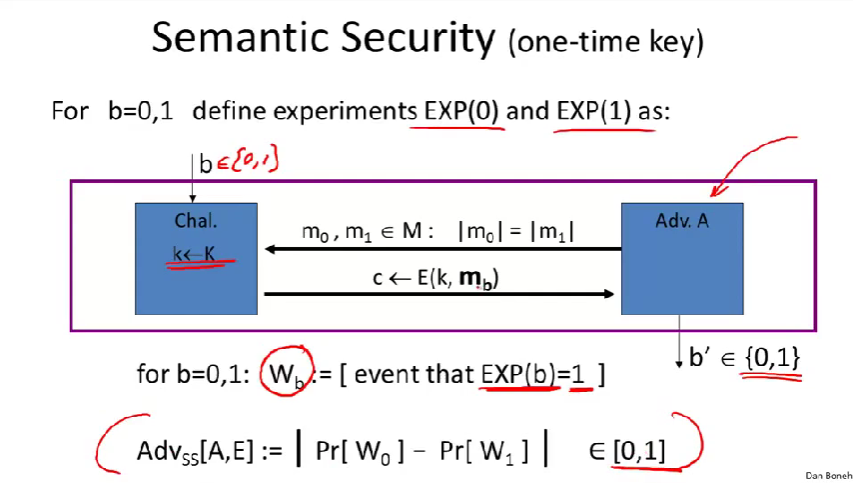
我们定义语义安全的方式通过两个实验,分别是实验0和实验1 。
b是0或1。
攻击者A所做的类似于对伪随机数发生器的统计测试。
挑战者:一个情况下按方式0输出,另一个情况下按方式1输出。
流程:
- 首先,挑战者选取一个随机密钥。
- 攻击者输出两个信息\(M_0\)和\(M_1\)。
- 然后挑战者输出\(M_0\)的加密结果(或\(M_1\)的加密结果)。(在实验0里挑战者会输出\(M_0\)的加密,在实验1里挑战者会输出\(M_1\)的加密。)
- 然后攻击者试图去猜,他得到的是\(M_0\)的加密还是\(M_1\)的加密。
定义事件\(W_b\)为在实验b中,攻击者输出1的所有事件。所以\(W_0\)中的事件意为在实验0中攻击者输出1,\(W_1\)意为在实验1中输出1。
优势解读:换句话说,我们看攻击者的行为是否有所不同,当给他\(M_0\)的加密,和给他\(M_1\)的加密。
在这些实验中,如果在两个实验中,攻击者以同样的概率输出1,就意味着攻击者无法区分两个实验。(优势是概率差,如果优势接近0,意味着攻击者无法区分实验0和实验,如果优势接近于1,意味着攻击者能很好地区分实验0和实验1)

如果对于所有有效的攻击者,优势可忽略。
现在假设有个被破解的加密机制。即对于攻击者A来说,给定密文,他总能推断出明文的最低位。

我们看为什么这个系统不是语义安全的。
我们是算法B,算法B里面用到了算法A。
- 首先是挑战者随机选取了一个密钥,我们首先需要输出两个明文,一个明文以0结尾,一个明文以1结尾。
- 挑战者将为我们加密\(M_0\)或\(M_1\),这取决于是实验0还是实验1。
- 然后我们就把得到的密文给攻击者A。对于攻击者A来说,给定密文,攻击者A可以算出明文最低位。(攻击者会输出\(M_0\)或\(M_1\)的最低位,即图中的位b)然后我们输出我们的猜测,记为\(b'\)。
优势是1,那么意味着攻击者完全破解了这个系统。
对于语义安全的密码,任一有效攻击者都无法揭露明文的一丁点信息,这就是完美安全的严格概念。
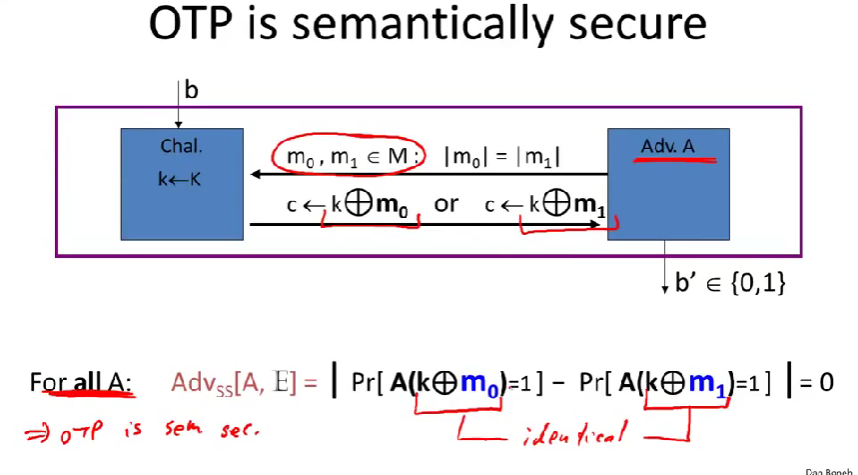
OTP是语义安全的,更甚至,它对任何攻击者都是语义安全的。
Stream ciphers are semantically secure
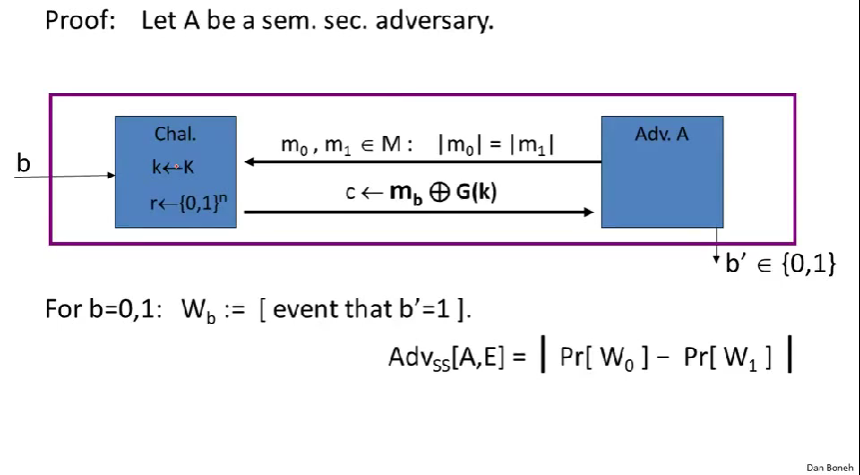
方法是证明它的逆否命题。
假设有一威胁语义安全的攻击者A,我们将构造一个PRG攻击者B以满足图中的不等式。
证明:由对于一个安全的发生器来说,一切有效统计测试都有可忽略的优势,所以右边是开忽略的,从而可以推出左边也是可忽略的。
即对于任一攻击者A,我们都能构造出一个攻击者B,我们知道攻击者B对发生器只有可忽略的优势,这就意味着A对流密码的优势也是可忽略的。(更自然地,如果A优势不可忽略,则我们能构造出B来破解PRG,即PRG不安全。)
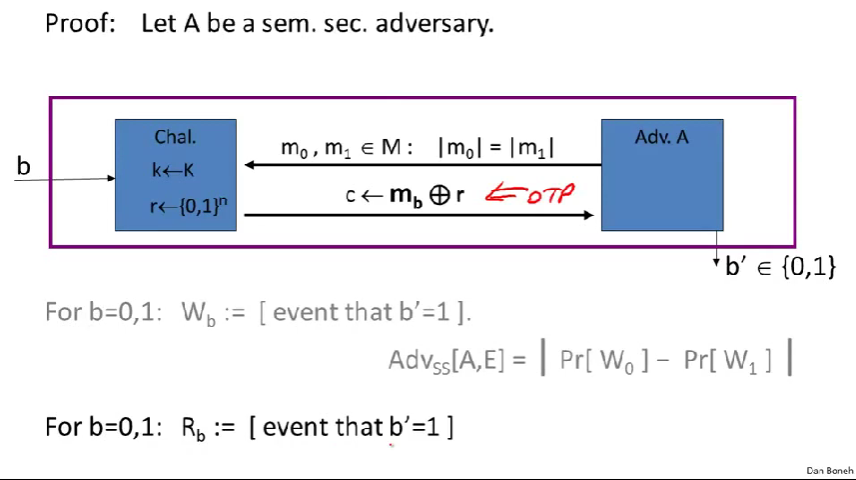
攻击者也无法区分密钥是否从PRG换成了r(即伪随机换成了真随机),一次性密码本是无条件地安全的,因此攻击者无法赢,这也意味着他不能赢下这个伪随机游戏。因此,最初的流密码一定是安全的。
W事件对应的伪随机,R事件对应的是真随机(一次性密码本)。

\(R_b\)即\(R_0\)或\(R_1\)。
存在攻击者B,使得这两个概率的差别就是B对发生器G的优势。(对这两个b都成立)

统计测试b:外部用n位字符串输入,输出判断随机或不随机(0或1)。
- 运行攻击者A,攻击者A输出两个信息\(M_0\)和\(M_1\)。
- 然后攻击者B回应,用\(M_0\)异或输入的字符串。
分组密码
What is a block cipher?
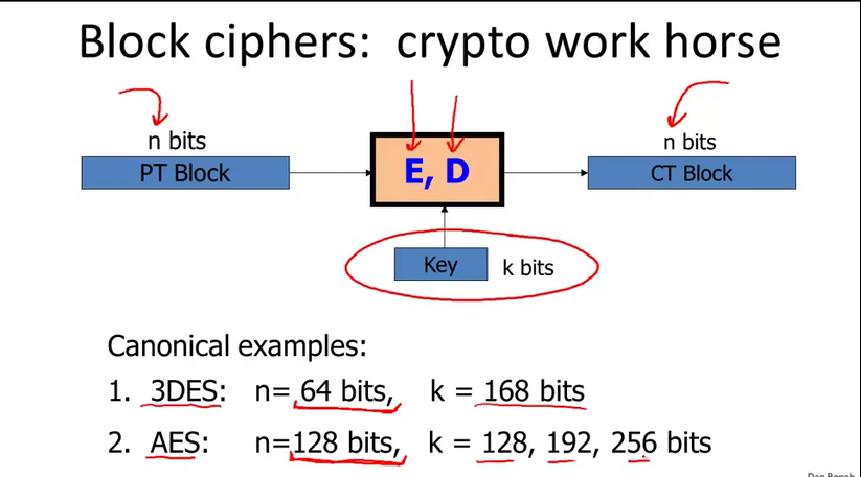
分组密码由加密和解密算法组成。它取n位明文作为输入,它的输出与输入具有严格相同的位数。
密钥越长,密码工作的速度越慢,但是也越安全。
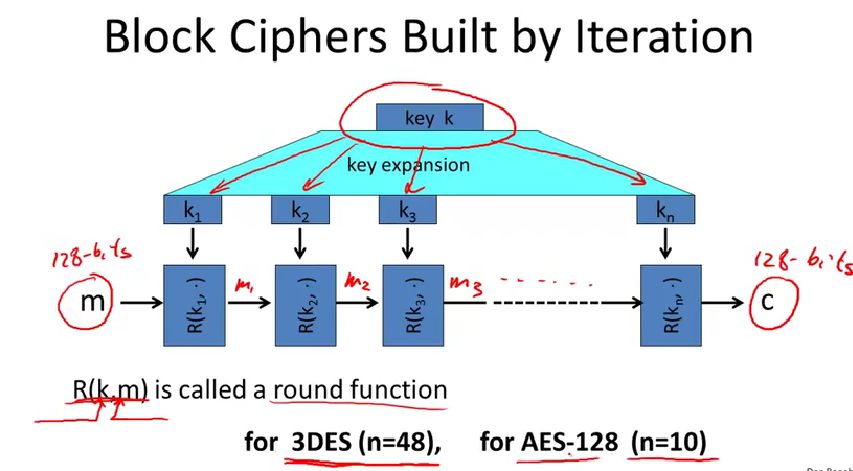
将密钥k扩展成一系列的回合密钥\(k_1\)和\(k_n\)。然后回合函数使用这些回合密钥一次又一次地迭代加密明文信息。
round function:回合函数。
3DES的回合数有48,而AES的回合数只有10。
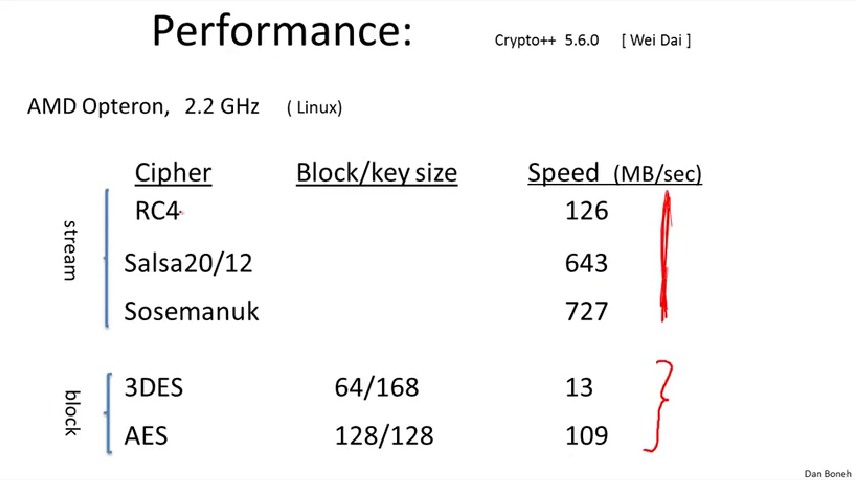
可以看出分组密码比流密码慢,但是分组密码能做很多事情。

Pseudo Random Function(PRF):伪随机函数
一个伪随机函数定义在密钥空间,输入空间和输出空间上,伪随机函数取一个密钥、输入,输出输出空间中的某个元素。(即它从K和X中各取一个元素,输出Y中的一个元素)
Pseudo Random Permutation(PRP):伪随机置换
它取密钥空间中的一个元素和X中的一个元素,输出X中的一个元素。
deterministic:确定的
一旦固定密钥k,函数E是一一对应的,所以也是可逆的。
要求有一个有效的逆向算法D,输入特定输出,会输出特定输出的原像。

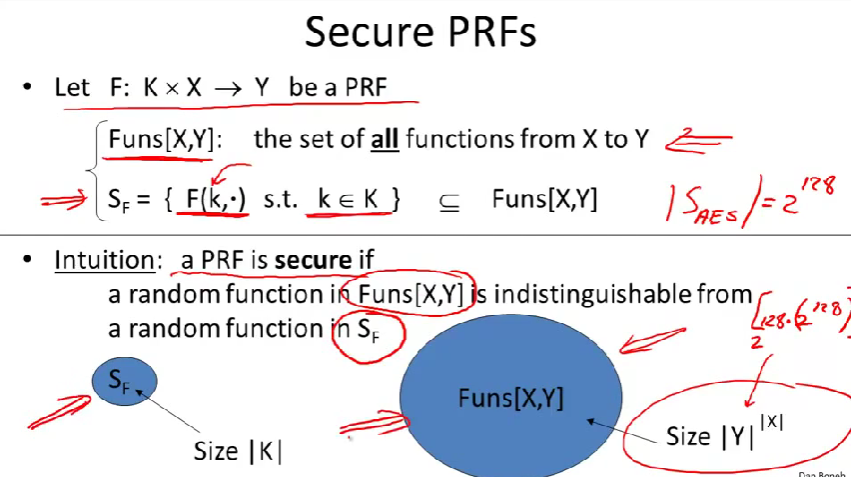
Funs[X, Y]是所有从集合X映射到集合Y的函数的集合。
Size\(|Y|^{|X|}\)的由来:对于每一个\(|X|\)的元素,映射到\(|Y|\)的方法有Y种,故大小即是将所有Y相乘。
让k不动,第二个参数浮动。
Size\(|K|\)的由来:由上面的Funcs[X, Y]的定义可知,我们具体分析其中的一个映射函数,它的每一个\(|X|\)的元素对应一个\(|Y|\)的元素,不然就不符合定义了。对于一个密钥k有一种映射方案,那么现在有\(|K|\)多个密钥,所以size是\(|K|\)。(举例:对于AES来说,\(Size_{AES}=2^{128}\))
PRF安全定义:
一个从X到Y的随机函数(这里指从Funs[X,Y]中任取一个函数)和从X到Y的伪随机函数(图中的\(S_F\))不可区分。
换句话说:伪随机函数集合上的均匀分布和全体函数上的均匀分布不可区分。
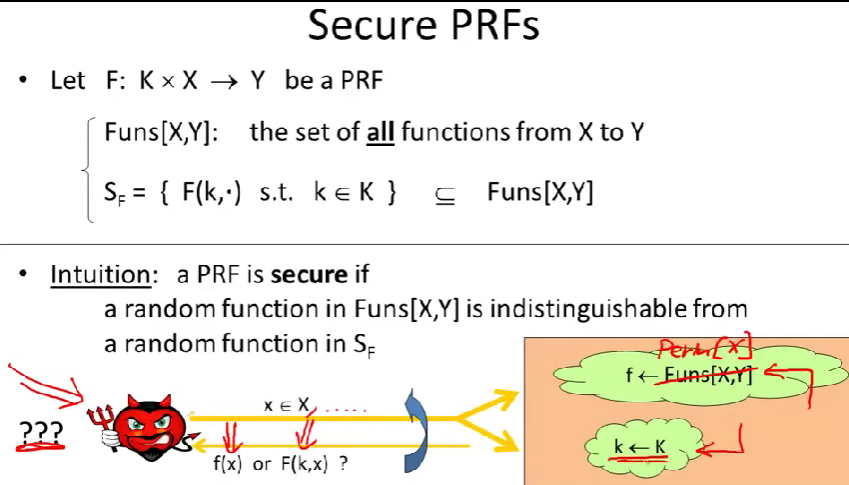
上面的云是一个随机函数。我们选择一个随机密钥,计算底端的伪随机函数。现在这个攻击者上传一些X中的点,对于他的每一个询问,会给他随机函数在点X处的值或是为随机函数在点x处的值,攻击者无法区分是哪一种。
例子:


parallelizable:可并行计算的
- 比如有两个处理器,让一个计算偶数位置(如图中的t=0、2......)的输出,另一个计算奇数位(如图中的t=1、3......)的输出。
- 很多流密码,比如RC4,是先天串行的。
安全性是由PRF的安全性得来的,(\(G(K)=F(0)||F(1)||...||F(t)\)是真随机函数的发生器。)
The data encryption standard(DES)
之前是讲解了key expansion的部分,这部分讲round function。
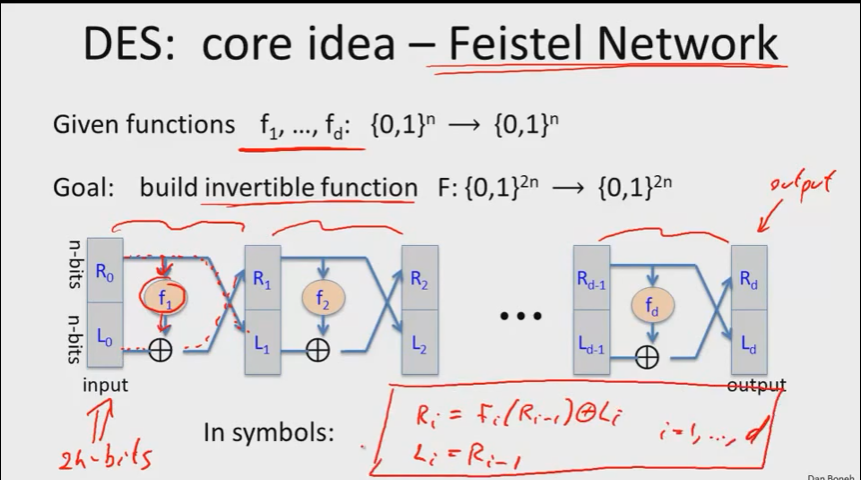
\(f_1\)和\(f_d\)是任意的函数,它们不一定是可逆的,我们要做的是根据这D个函数构造处一个可逆的函数。
\(R_0\)输入被被复制了一份,为\(f_1\)的输入(\(f_1(K_0,R_0)\)),结果和\(L_0\)异或,成了新的\(R_1\)。 \[ R_i=f_i(or\ R_{i-1})\oplus L_i\ ,i=1,2,..,d\\ L_i=R_{i-1} \]
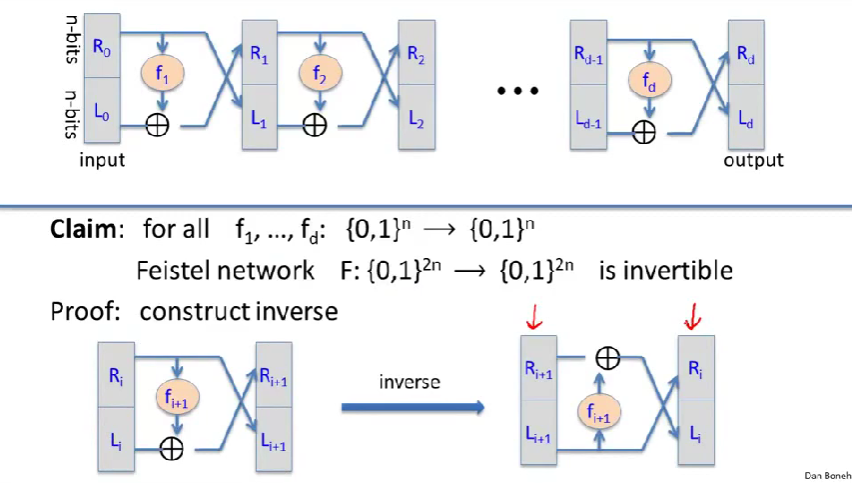
事实上,与给的函数\(f_1\)到\(f_d\)无关,最后构造出的函数是可逆的。
证明可逆:
先来看一回合的Feistel网络,这里输入\(R_i\)和\(L_i\),得到\(R_{i+1}\)和\(L_{i+1}\),然后问题是如何求逆。假设我们的输入是\(R_{i+1}\)和\(L_{i+1}\),想计算\(R_i\)和\(L_i\)。 \[ R_i=L_{i+1}\\ L_i=f_{i+1}(or\ L_{i+1})\oplus R_{i+1} \] 可以发现左边和右边是镜像的,
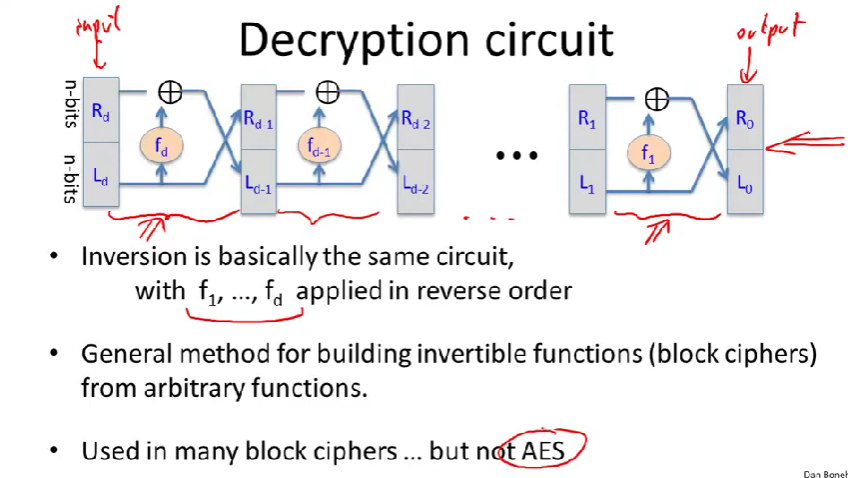
函数应用的顺序相反。
可以看到顺序也调换了,原先输入\(R_0\)是要被复制的,逆运算输入的\(R_d\)不用被复制。
chatgpt的解释:
实际应用中的处理
在实际应用中,顺序调换可以通过以下几种方式处理:
- 明确协议或标准: 在设计加密协议或标准时,明确规定输入和输出的顺序。解密时,接收方知道需要交换顺序才能得到正确的明文。
- 自动交换: 在实现加密算法的库中,自动处理顺序调换。例如,在解密函数中最后一步自动交换得到的左右部分。
- 文档说明: 在算法实现的文档中明确说明这一点,使用者在调用加密和解密函数时需要注意顺序问题。
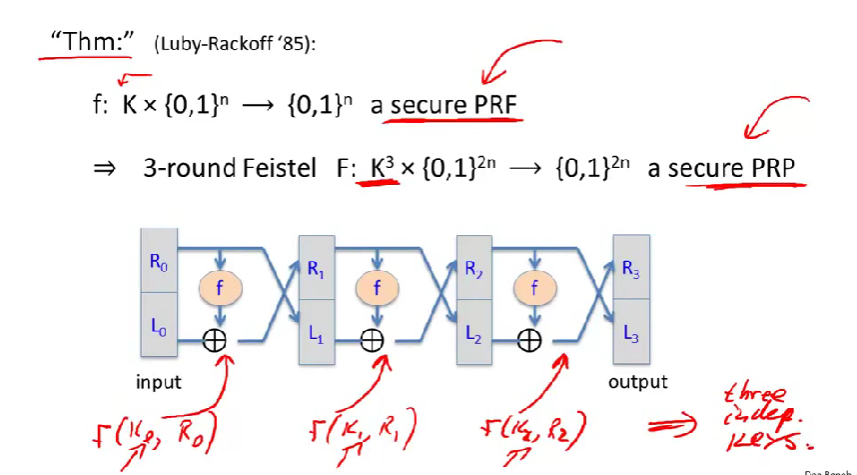
一个关于Feistel网络的重要定理,用来证明Feistel网络是个好办法。
\(K_0\)、\(K_1\)、\(K_2\)是独立的三个密钥。
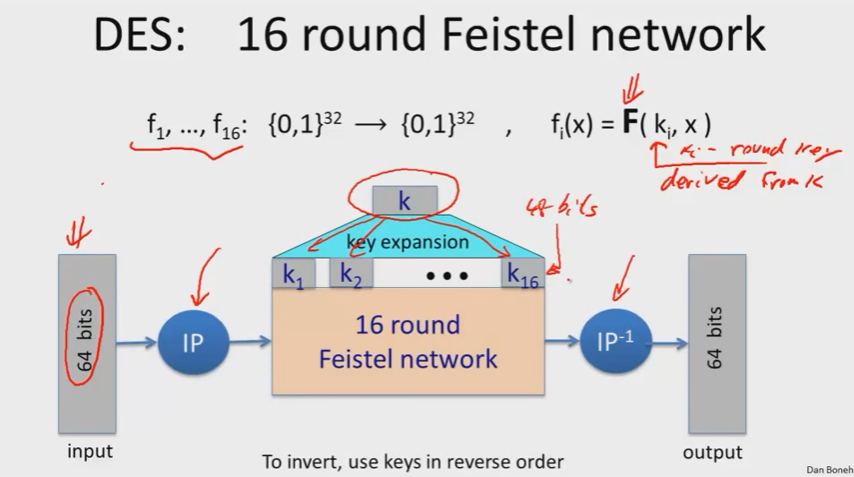
DES有16回合的Feistel网络。
IP(initial permutation):初始置换,置换这64位,比如将第0位置换到第6位,第2位置换到第18位等。
\(IP^{-1}\):初始置换的逆置换。
56位的DES密钥k被扩张成了这些回合密钥。(16个48位的回合密钥)
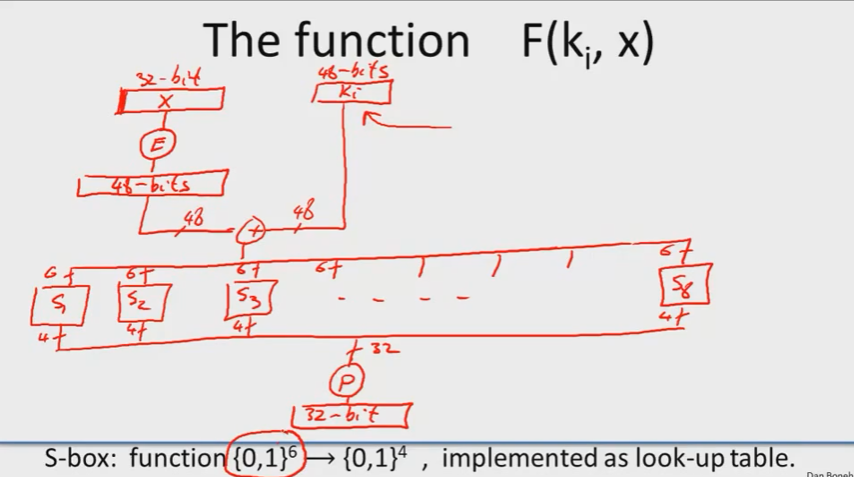
\(F(k_i,x)\),x是\(R_0,R_1,R_2,R_3\)等,有32位,密钥\(k_i\)有48位。
过程:
- x先进去一个扩张盒子,映射搭配48位字符串。(扩展盒子干的事情是复制某些位,移动其他位)
- 扩张后的x和\(k_i\)异或。
- 异或后的结果被分解成8组,每组6位,然后分别进入S盒(\(S_1...S_8\),S盒是一个6位到4位的映射)。
- 每个S盒输出的4位最后被收集起来,形成了32位,然后再经历一个置换,最终得到了函数F的输出32位。

S盒:取两边作为一个索引,其余中间四位作为一个索引。
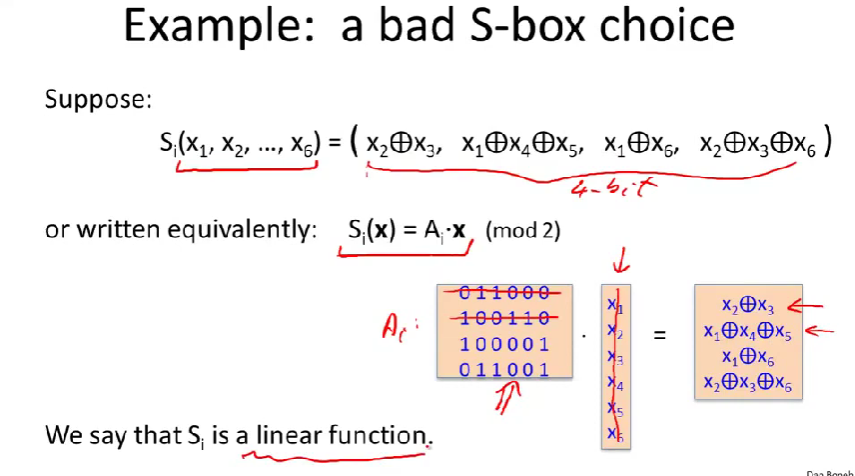
要弄明白S盒为什么要这样设计?
假设S盒是一种线性的方式,仅仅是将6位输入以不同方式进行异或,然后输出4位。另一种表示方法是可以将S盒写成矩阵向量积的形式,那么可以表示成该矩阵向量与一个6位的向量内积再模2的形式。(异或就等于每一位相加模2)
我们仅仅做的是将矩阵A应用到向量X上,所以我们说,这时S盒是完全线性的。
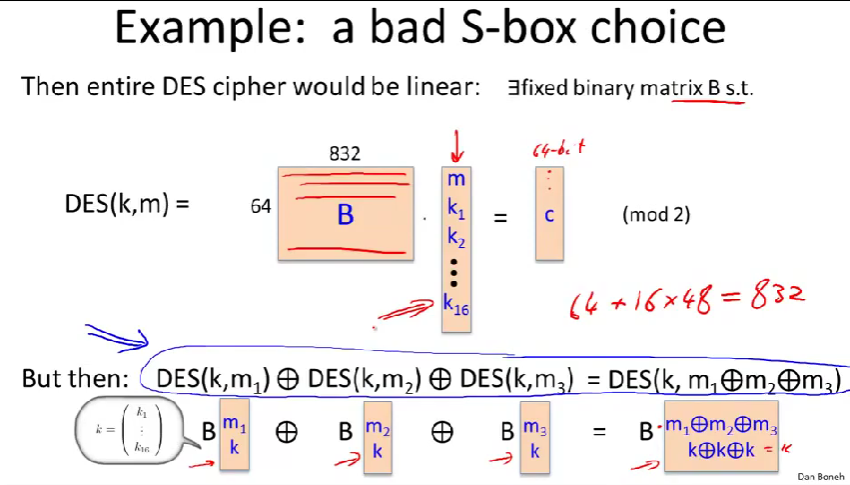
如果S盒是线性的,DES将一点都不安全。
原因:
- 那么DES所做的就是异或和置换,因此所有DES都只是一个线性函数。那么存在一个矩阵B使得与\(m、k_1、k_2...k_{16}\)所组成的向量的向量积是密文的各个位的值。(\(64 + 16\times48=832\))
一个简单的例子:
计算3个DES的输出的异或。得到了三个明文异或的加密结果。一个随机函数是不应该满足这个等式的。(或者说,以极小概率成立)
如果给出足够的输入、输出对,是可以还原出整个密钥的。比如,本例如果给出832个输入、输出对,就可以还原出整个密钥。

实际上,如果DES和线性相近,也足以破解DES了。特别的,如果你随机地选择S盒子里的值,实际上结果还是有些接近于线性函数的。这样还是可以破解DES,还原密钥的。
S-boxes are 4-to-1 maps:每个输出都有4个原像。
Exhaustive Search Attacks
Exhaustive Search Attacks:穷举攻击

目标是对给出的输入输出对(\(m_i,\ c_i\)),找出完成这些映射的密钥。
Question 1:
how do we know that this key is unique?
in fact just one pair is enough to completely constrain a DES key.
proof:
引理:假设DES是一个理想的密码(对于每一个密钥,DES都实现了一个随机可逆函数,由于DES有\(2^{56}\)个可能的密钥,我们假定DES是\(2^{56}\)个函数的集合,它们在64位字符串上可逆。)
我们知道c=DES(k, m)的可能性有多大,但我们要问
\(Pr[\exist k^\prime\neq k:c=DES(k,m)=DES(k^\prime,m)]\)
如果存在这样的\(k^{\prime}\),那么对给定的m和c,我们无法确定正确的密钥是k还是\(k^{\prime}\)。
可以通过遍历所有密钥来看满足它的可能性有多大(从第一个密钥,全0密钥,一直往后)
由联合边界,显然这个概率是小于每个密钥的概率相加的。
- 联合边界(The union bound)引理:令A1, A2, ..., Ak为k个不同的随机事件,那么:
\[ P(A_1 \bigcup...\bigcup A_k)\le P(A_1)+...+P(A_k) \]
比如抛三枚硬币都是正面的概率是小于等于1的(概率小于等于1),而概率相加可能大于1。
即: \[ Pr[\exist k^\prime\neq k:c=DES(k,m)=DES(k^\prime,m)]\le\sum_{k^\prime\in\{0,1\}^{56}}Pr[DES(k,m)=DES(k^\prime,m)] \] 假设固定\(k^\prime\),则概率最多为\(\frac{1}{2^{64}}\)(排列有\(2^{64}\)个可能的输出),由于有\(2^{56}\)个可能的密钥,所以再与其相乘。 \[ Pr[\exist k^\prime\neq k:c=DES(k,m)=DES(k^\prime,m)]\le\sum_{k^\prime\in\{0,1\}^{56}}Pr[DES(k,m)=DES(k^\prime,m)]\\\le2^{56}\cdot\frac{1}{2^{64}}=\frac{1}{2^8}=\frac{1}{256} \] 所以密钥不是唯一性的概率是\(\le\frac{1}{256}\)的概率,因此其唯一性的概率是\(\ge1-\frac{1}{256}\approx99.5\%\)
Question 2:
There's only one key that will map that plaintext to that ciphertext, and the question is just, can you find that key?

unicity prob. :“Unicity probability” 是一个概率论中的概念,用于描述某一特定事件在特定条件下是唯一发生的概率。

DES challenge:一个针对DES的挑战赛,主办方给了给了三对明文密文对(如图,\(c_1、c_2、c_3\)),以及若干密文(如图,\(c_4、c_5、c_6...\))。
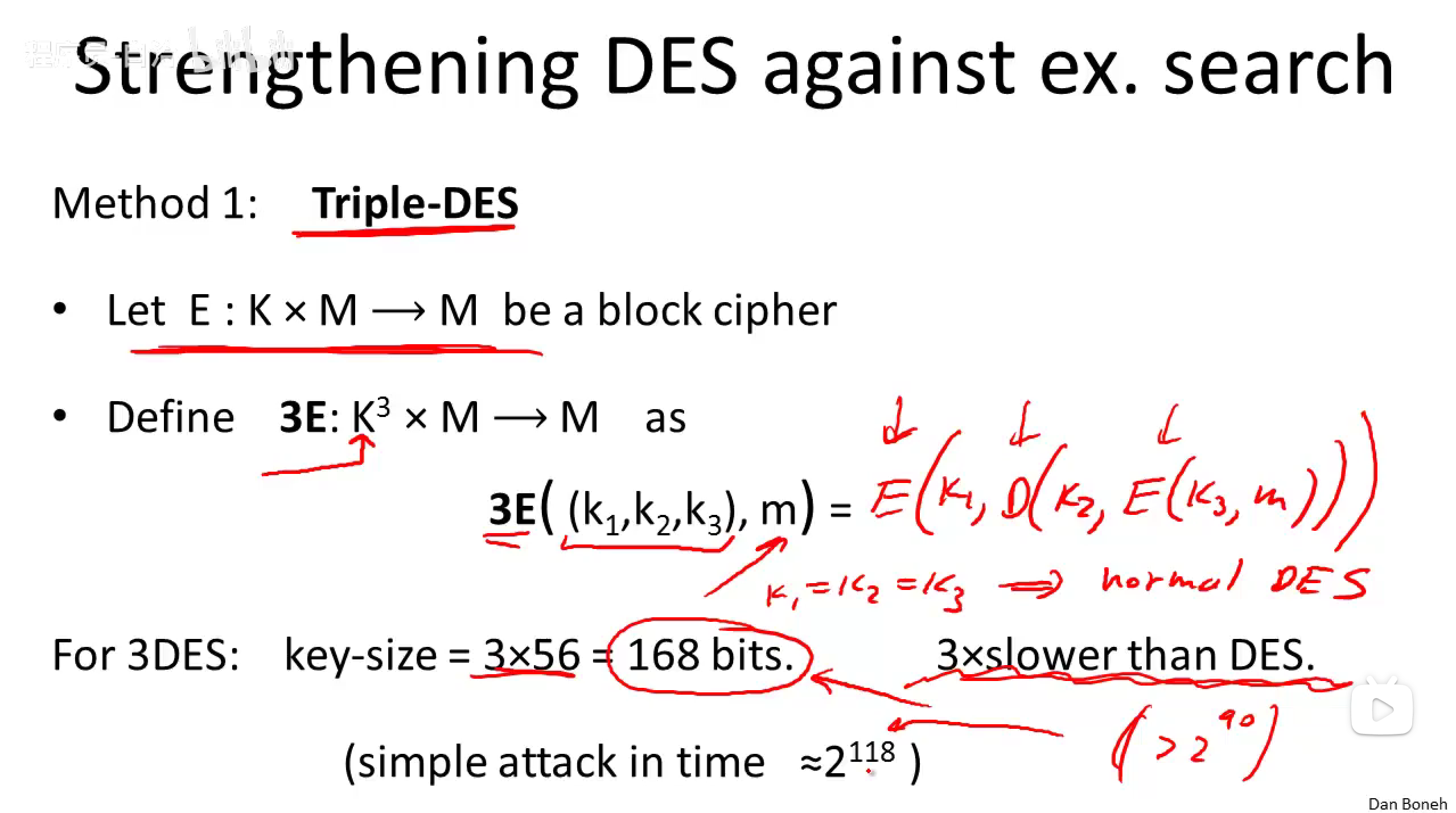
3DES,三重结构使用三个独立的密钥,三个独立的密钥加密三次。
\(3E((k_1,k_2,k_3),m)=E(k_1,D(k_2,E(k_3, m)))\)
为什么使用EDE,不用EEE ?
- 兼容DES
- 采用EDE主要为了与被广泛应用的DES算法保持兼容性,让3DES使用者能够解密原来单纯DES使用者加密的数据,即实现3DES与单密钥DES系统的通信,在实现过程中只需要令K1=K2。
3DES破解需要的时间\(2^{168}\)(但事实上,有一个简单的攻击可以在\(2^{118}\)时间内运行),实际上,大于\(2^{90}\)已经足够安全了。
缺点:速度太慢,是DES的三倍慢。

Question: why not repeat the cipher just two times? or in particular, the question is, what's wrong with the double DES?
\[ E(k_1,E(k_2,m))=C\\ \Rightarrow E(k_2,m)=D(k_1,c) \]
Meet-in-the-middl attack:中间相遇攻击。
我们将变量分成两边,两边同时开始。这样意味着攻击比详尽搜索(穷举搜索)更快,这种攻击被称为中间相遇攻击。
攻击步骤:
- 对于每一个密钥(总共有\(2^{56}\)),计算出加密结果,然后排序(时间nlogn),建立一张表。
- 总时间是nlogn,因为计算的步骤可以放在排序里面完成。
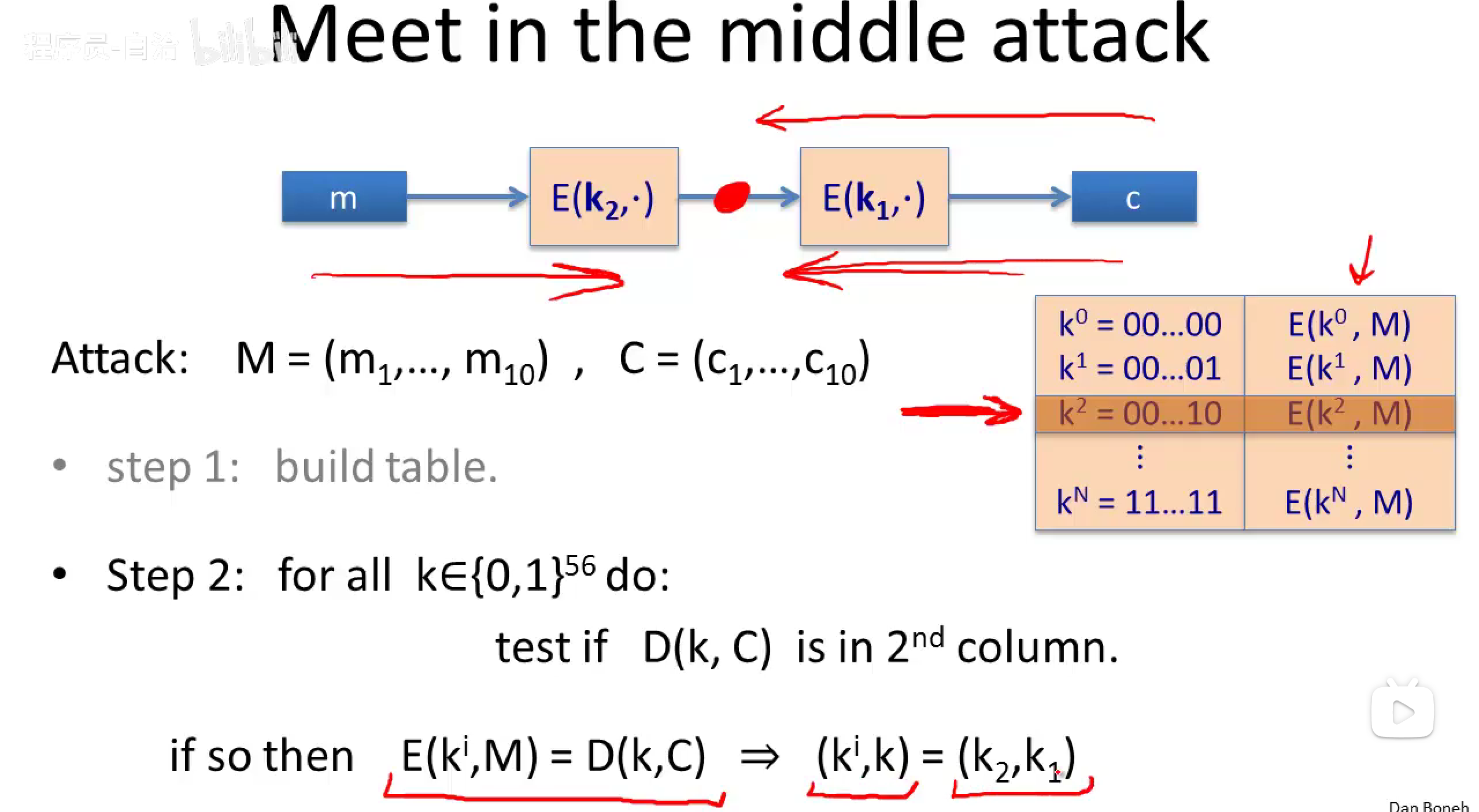
- 然后对表中左列的每个密钥,依次实行解密,判断结果是否在右边那列中(时间nlogn)。
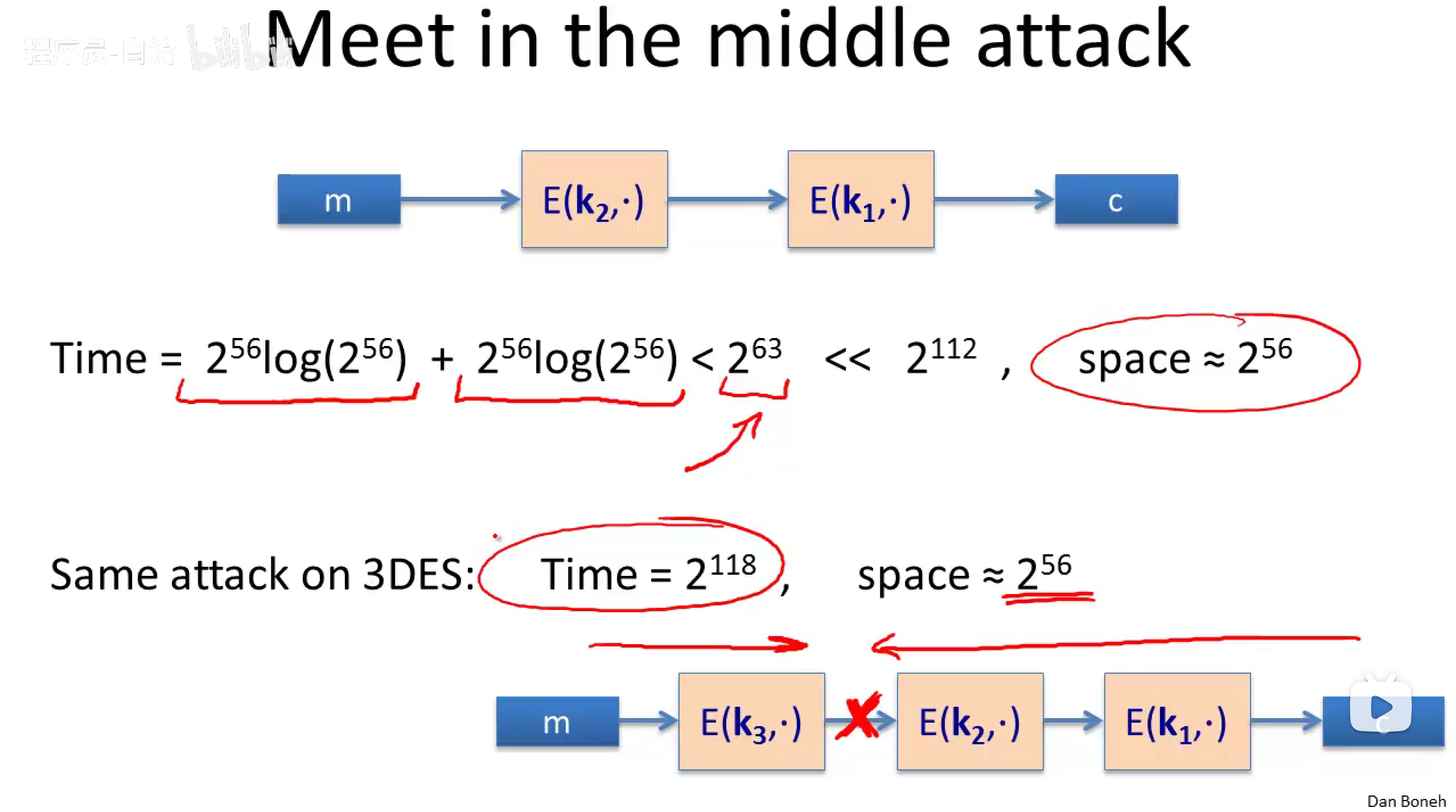
nlogn+nlogn(加密排序制表的时间+解密查找的时间)

防范详尽搜索的改造:DESX(但是无法防范对DES更微妙的攻击)
定义EX结构
有两个密钥和区块大小一样长(64位),还有一个和密钥大小(56位)一样长。
实际上,已知最好的攻击需要\(2^{120}\)时间。(通用的攻击,微妙的攻击不知道)
只在外面做异或或只在里面做异或,对保护密码无济于事。
More attacks on block ciphers

side channel attack:旁路攻击(侧信道攻击、边信道攻击、旁道攻击)
基于分组密码实现上的攻击。
设想你有一个智能卡,上面实现了一个分组密码,可以用来支付。当你把卡插入支付终端里,如果一个攻击者获得了你的智能卡,他可以将这张卡拿到实验室里,然后运行这张卡,非常精确地测量这张卡加密和解密的时间。(加密和解密的时间取决于密钥的内容。)通过测量时间,攻击者可以学习到你的密钥内容。事实上,他可能可以完全提取出你的密钥。
有很多例子是通过非常精确地测量加密算法的时间来提取密钥的。
另一个例子不是测量时间,而是测量功耗,当卡运行时的功耗。可以联结一个设备,用来测量智能卡需要的电流,然后非常精确地记录电流,这些智能卡不是非常快, 因此你可以测量每个时钟周期内的精确功耗。比如得到上图中的图表。
前面和后面分别是初始置换和最终置换的时候,中间有14个峰值和谷,分别对应16轮回合函数。(甚至发大这张图,你可以一位一位读出来)
实际上,即使智能卡采取措施来屏蔽这种信息,它依然是脆弱的,有一种攻击叫做差分功耗分析,运行加密算法很多次,测量智能卡功耗,只要有电流上的小差异,密钥各位的依赖性,在经过足够多的加密算法运行次数就能显现出来。
设想一个多核处理器,其中一核运行加密算法,而攻击者代码却同时在另一核上运行。现在这些代码共享同一缓存,于是攻击者可以管理观测加密算法带来的缓存缺失。实际上通过观察这些缓存缺失,可以完全解出算法使用的密钥。
fault attacks:错误攻击
攻击智能卡时,可以造成智能卡异常工作,可以调高时钟频率,可以加热芯片,你可以让这个处理器异常工作,输出错误的数据。实际上加密时,最后一回合有错误,产生的密文就可以暴露密钥k了。
- 抵抗这种攻击,意味着在暑促算法结果前,应当检查以确保计算结果的正确性。

给很多很多输入输出对,能否比穷举攻击更好地还原出密钥?
Linear cryptanalysis:线性密码分析
逐位异或一组明文比特,异或特定的一组密文比特,然后和相应密钥比特的异或进行对比。如果两者严格独立,那么概率是\(\frac{1}{2}\)。(因为所有异或要么是0,要么就是1,所以概率是\(\frac{1}{2}\))
设想有一点不均匀导致这个等式以概率\(\frac{1}{2}+\epsilon\)成立。(事实上,对于DES来说有这么个关系,因为第5个S盒子的设计有点太接近线性函数了)
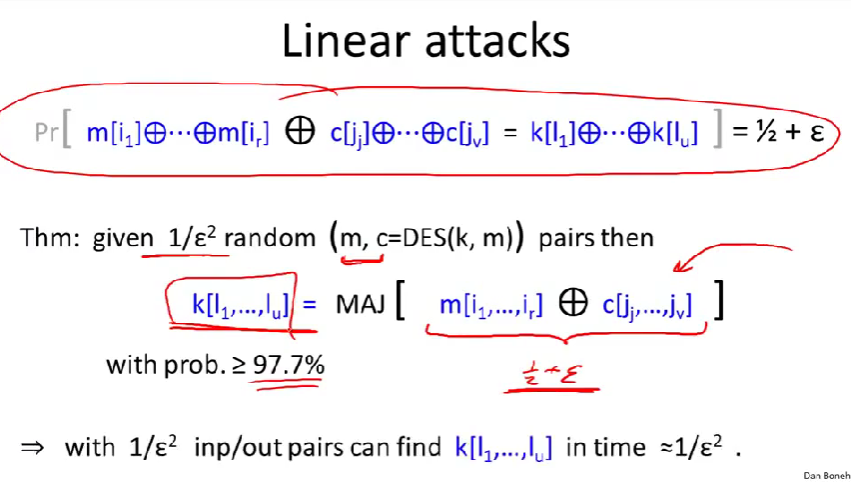
可以使用像这样的一个方程来决定某些位。假设你有\(\frac{1}{\epsilon^{2}}\)那么多个明文密文对,这些必须是互相独立的随机明文和对应密文,应用这上面的公式,因为有\(\frac{1}{2}+\epsilon\)的概率,明文和密文各比特异或再异或的结果等于密钥各比特异或的结果。我们可以取全部明文和密文对计算值中的大多数,这个结果和密钥各比特异或相等的结果的概率是\(\ge97.7\%\)的。

应用到DES上,使用这个方法,你不仅仅只得到密钥中的一位,事实上,你得到两位。一个往前,一个往后,这样就给你密钥这两位的异或值了。实际上,还能获得其余12位,因为可以解出第5个S盒子的输入。
接下来需要做的就是穷举密钥中剩下的位即可。(攻击的第一步,确定14位需要\(2^{42}\)的时间,剩下位的穷举需要另一个\(2^{42}\)的时间)

教训:任一细微的线性关系都会引入线性攻击。

Quantum attacks:量子攻击(它对分组密码是通用的)
假设有一个定义在大集合X上的函数,输出有两种值,0或1,这个函数的值大部分都是0,目标是找出这些输入,满足函数值为1。
用量子计算机,解决这搜索问题,用不着|X|的时间,而是|X|的平方根的时间即可。

其实把攻击DES的过程看做f(k),那么使用量子计算机则只需要花费\(O(|x|^{\frac{1}{2}})\)的时间就能破解DES。
如果有量子计算机,破解AES-128只需要\(2^{64}\)的时间,也是不安全的。那么应该使用256位密钥大的算法了,比如AES-56
。
The AES block cipher
AES(Advanced Encryption Standard):高级加密标准

有3钟密钥长度:128、192、256,分组大小是128。
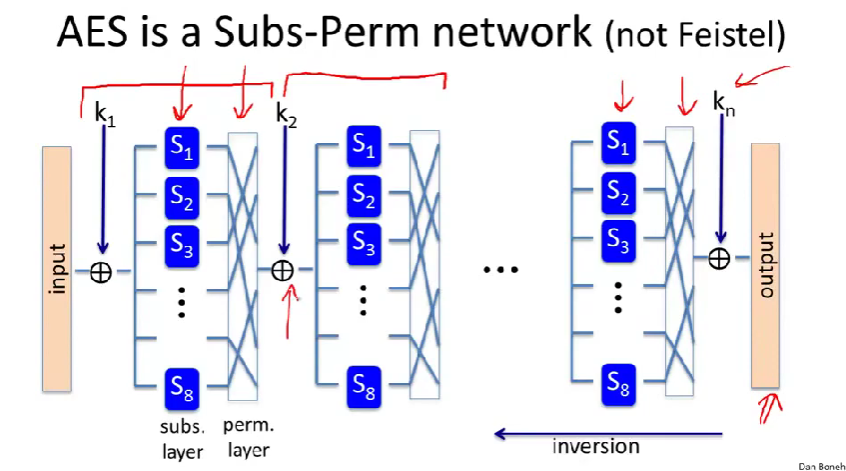
AES网络的每一步都可逆,所以整个过程都是可逆的。
AES的代换层是可逆的,这和DES非常不同,DES的代换完全是不可逆的,它们将6位映射到4位。
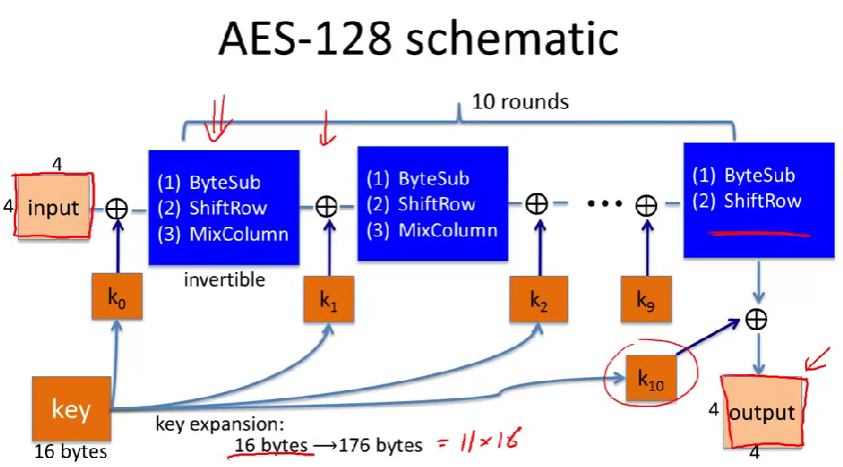
\(4\times4\)矩阵,16个字节,128位。
密钥扩展。

- ByteSub:字节代换ByteSub是一个包含256个字节的S盒。对当前状态里的每一个字节应用S盒(或者说,A表)。\(\forall i,j, \ A[i,j]\leftarrow S[A[i,j]]\)。
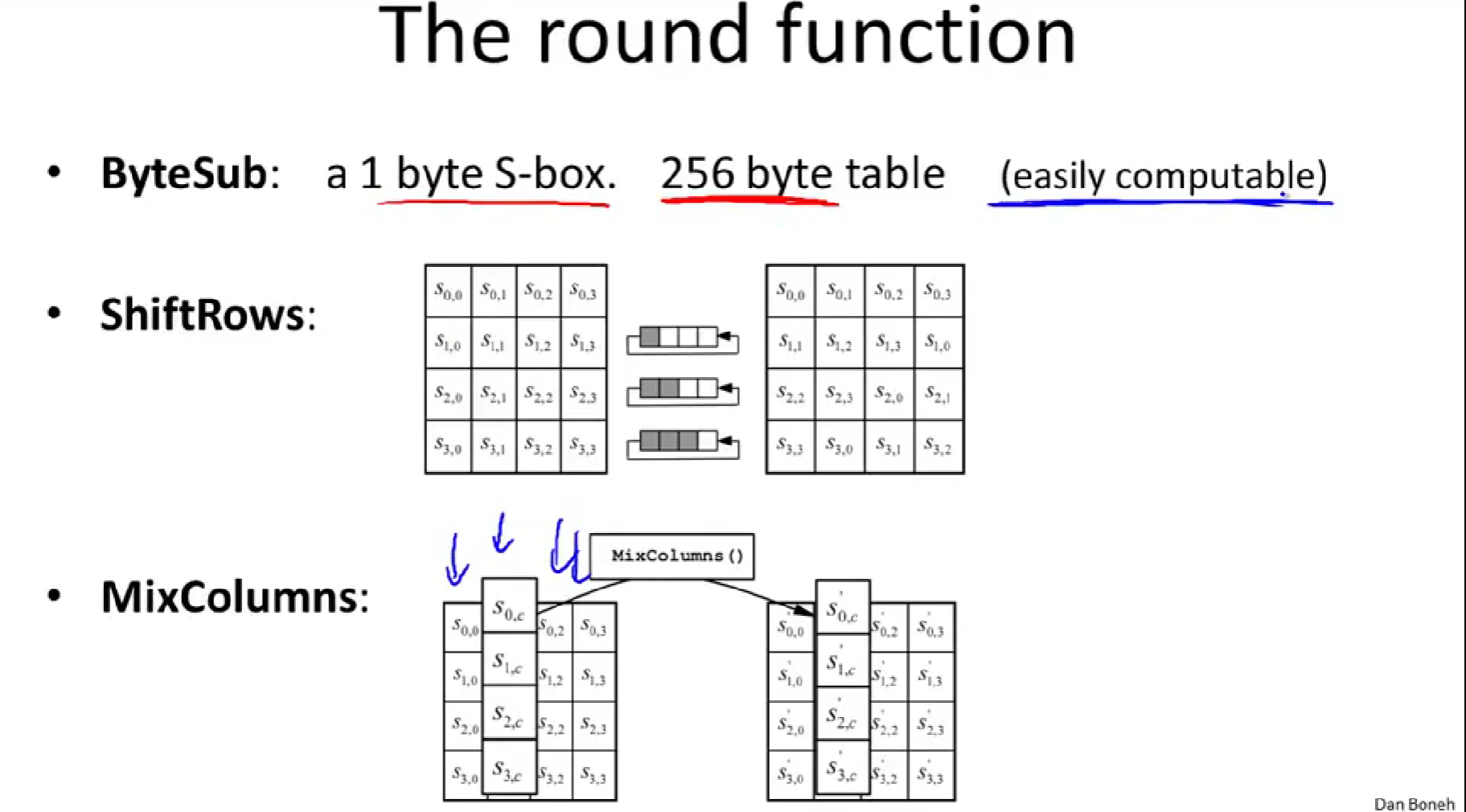
- ShiftRow:对每一行的四个字节整体移动。(比如图中,第二行被平移了一位。)
- MixColumns:一个线性变换,对每一列进行变换。将一特定的矩阵乘以每一列的向量,得到新的列。

Pre-compute round functions(24KB or 4KB):比如可以将上面三步转换成代换表,或者更长的。(由于只需要查表和异或,不需要进行复杂的数值计算,因此速度会很快)
Pre-compute S-box only(256 bytes):预先计算好S盒,S盒大小是\(16\times16=256\)字节。
No pre-computation:全部即时计算。
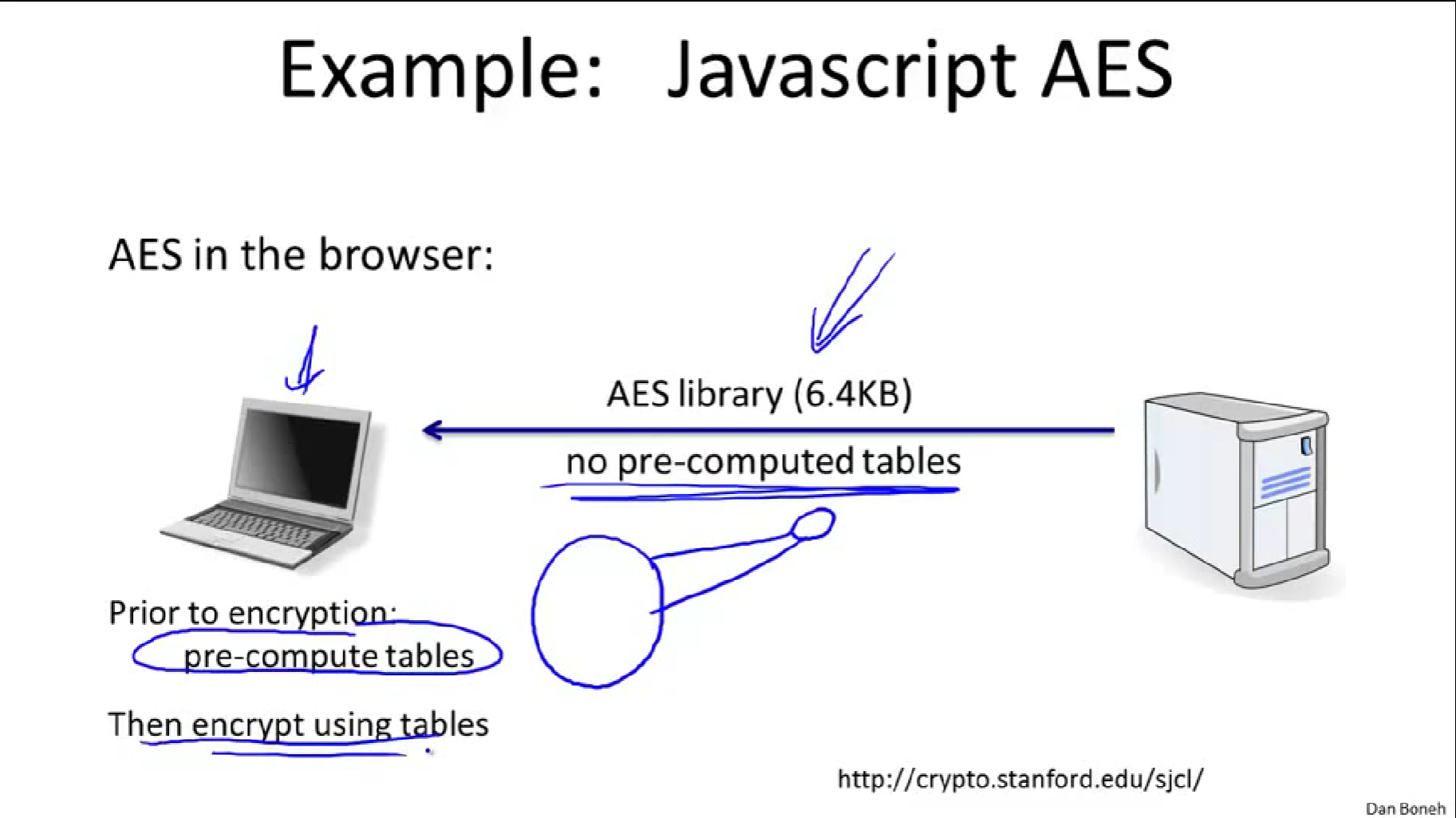
一个不同的例子。假设用JavaScript实现AES,将AES库发给浏览器,这样浏览器就能使用AES,目标是要减少代码大小,使得发给浏览器的网络传输的流量较小,同时又要让浏览器的性能尽可能地快。
解决办法是发送给浏览器的代码不包含任何预先计算的表,代码体积较小,但当代码到达浏览器时,浏览器会预先计算所有的表,然后表可以存在电脑上。

在硬件上实现AES
aesnc实现了AES的一轮加密,用回合密钥和明文异或,再应用三个函数;aesenclast实现了AES的最后一回合加密,最后一回合不含MixColumn,只有ByteSub和ShiftRows。
- 这些指令使用128位寄存器,对应AES的状态,会有一个寄存器包含状态值,另一个寄存器包含当前回合密钥,当调用AES时,使用这两寄存器,运行一回合的AES,然后把结果存到这个XMM里面的一个状态寄存器中。
- 如果需要实现整个AES,需要调用aesnc9次,再调用一次aesnclast。

最好的还原密钥攻击:比穷举快4倍,需要\(2^{126}\)时间。
实际上,AES256的密钥扩张的设计有弱点,会导致相关密钥攻击。
相关密钥攻击:如果给我大约\(2^{100}\)个AES的输入输出对,但是是有4个相关联的密钥得来的,这些密钥之间关系密切(海明距离非常短),那么需要\(2^{99}\)时间。(比穷举攻击的时间好太多了)
Block ciphers from PRGs
本节研究是否能从更简单的原型,比如伪随机数发生器,来构建分组密码。

首先,我们研究是否可以从伪随机数发生器构建伪随机函数, 而不是伪随机置换。
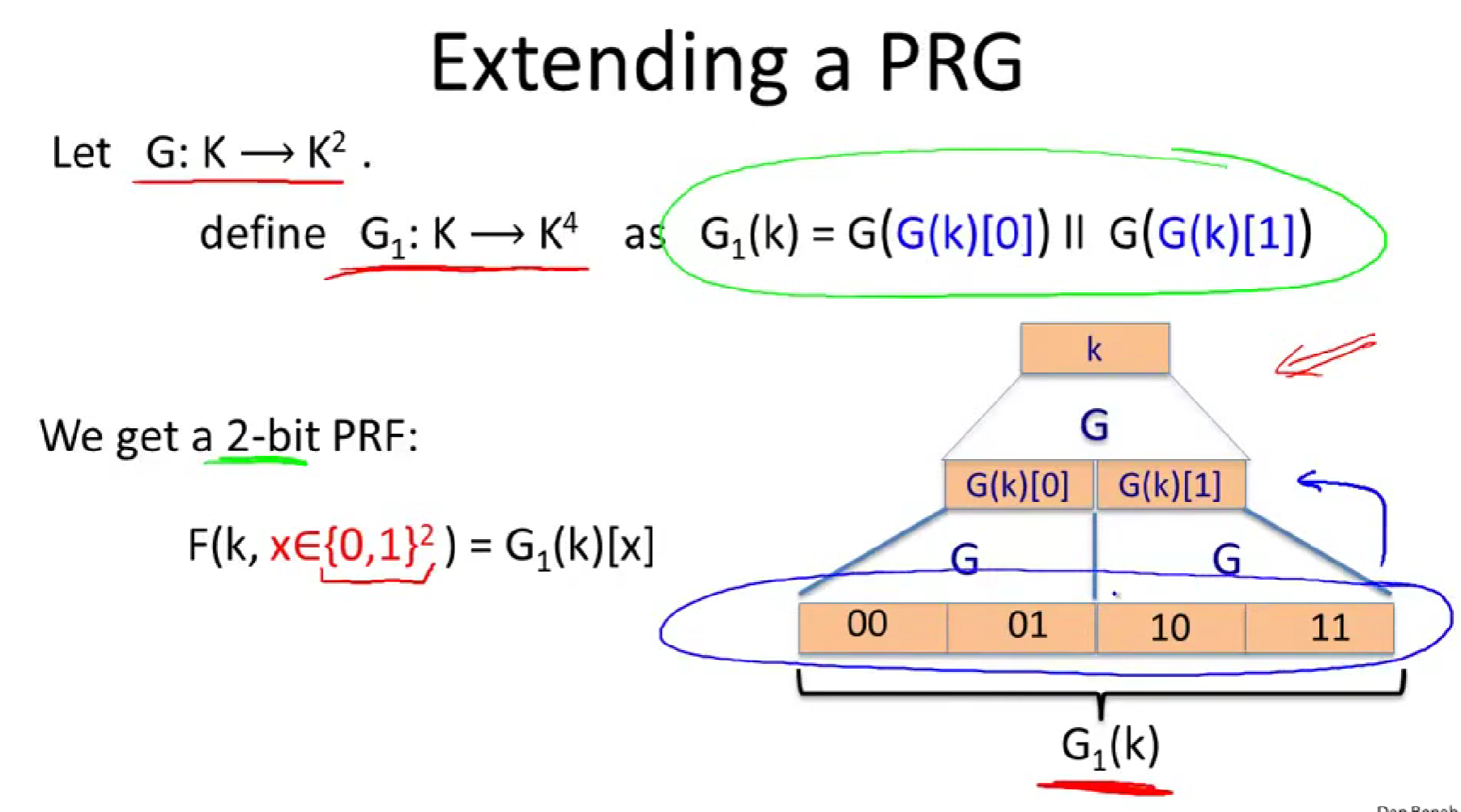
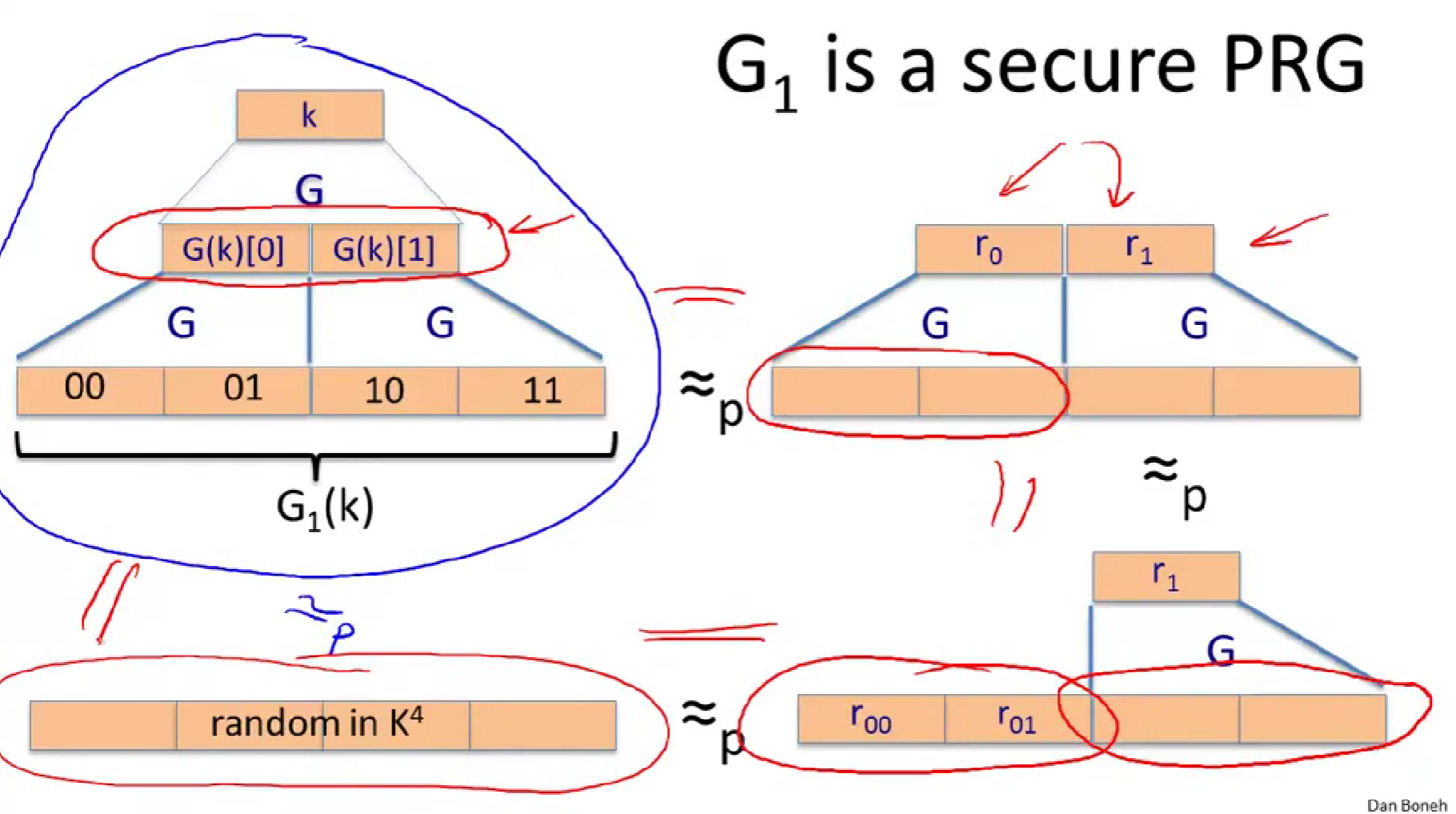
证明:用真随机来替换第一层,(由PRG的定义,它的输出和真随机的输出不可区分。)
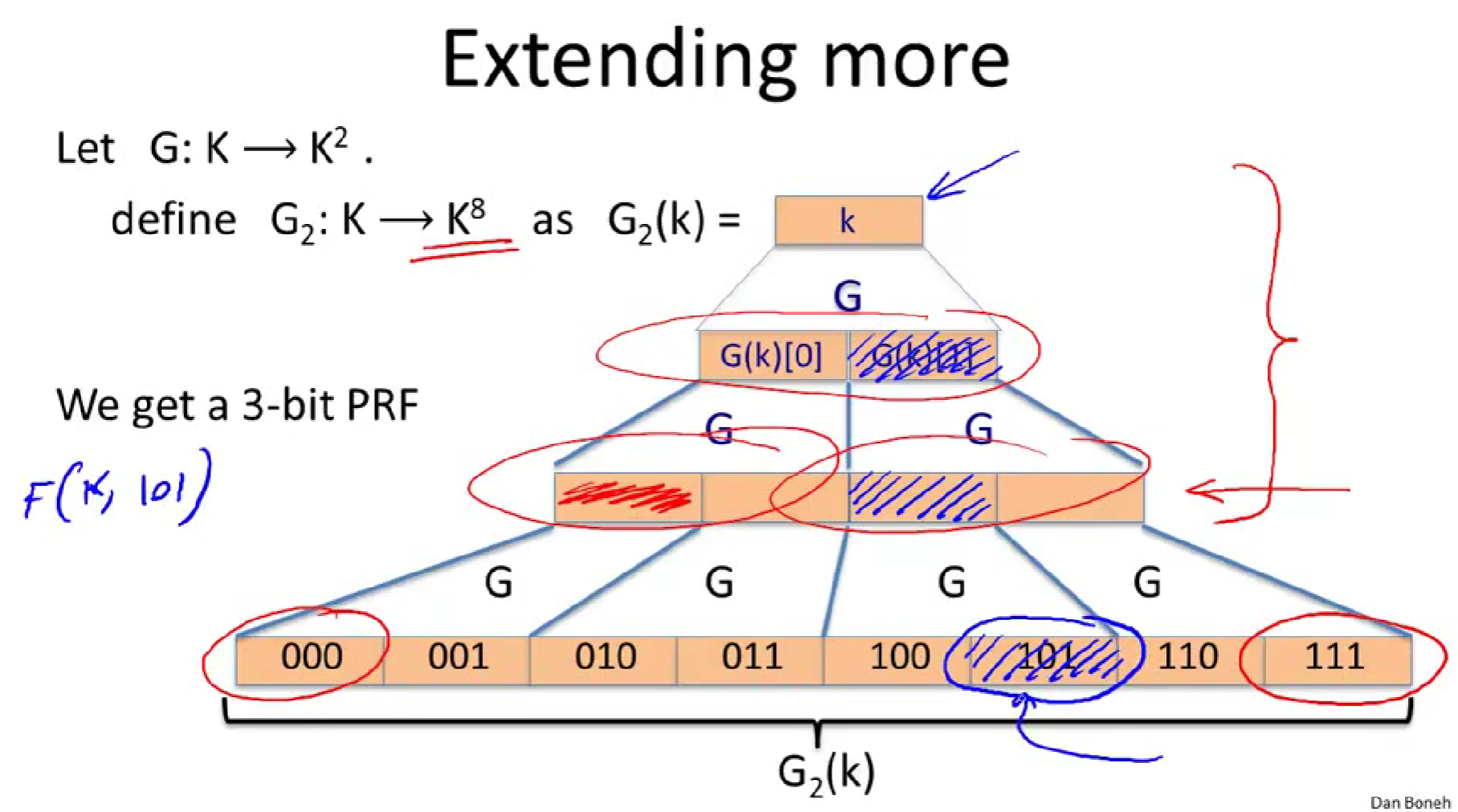
比如我们获得了3为PRF,假设我们想计算PRF在101处的值,我们从这个初始密钥k出发,应用发生器G,但只关心G输出的右边,然后再应用发生器G,只关心左边,以此类推。
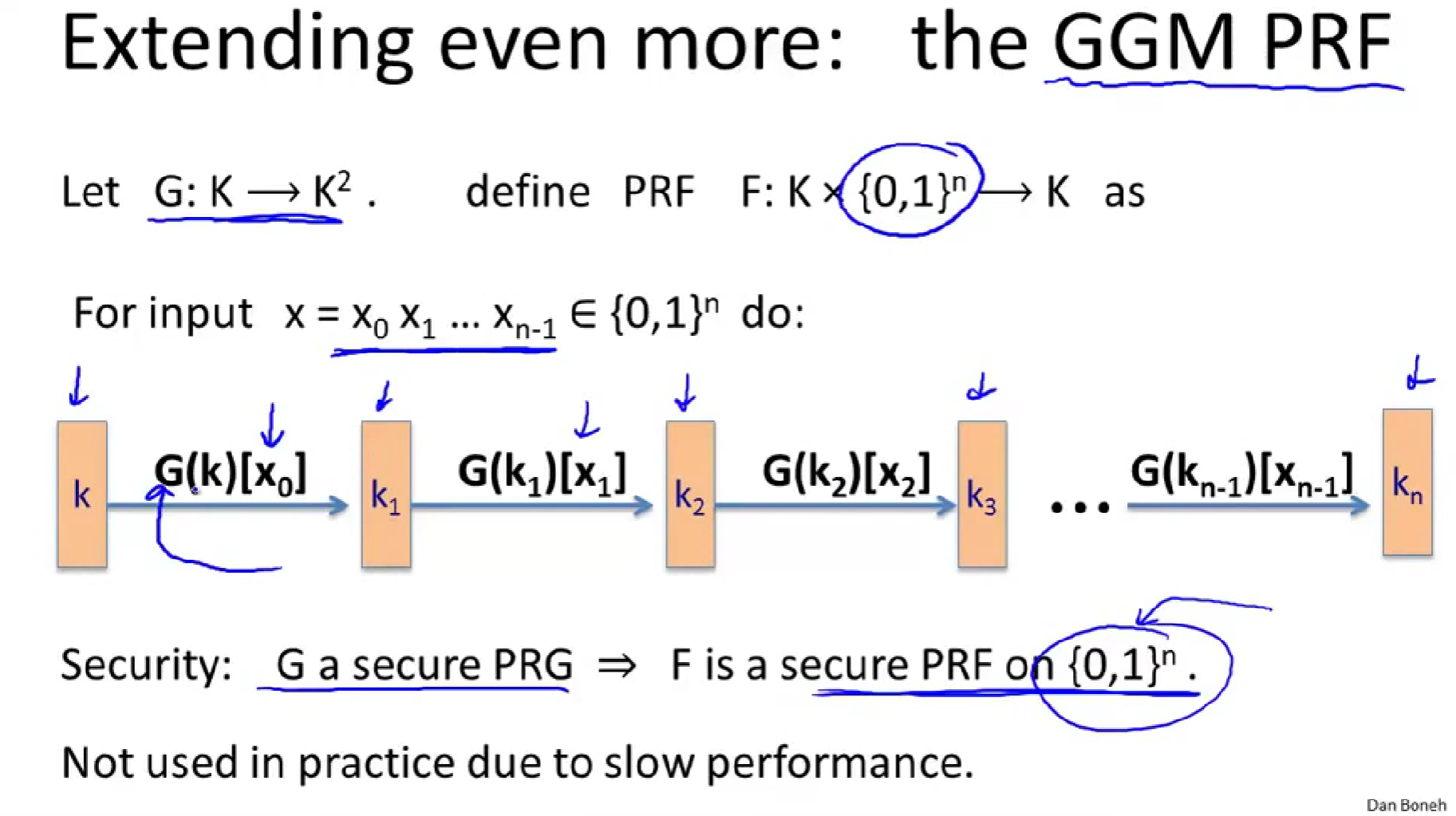
GGM是这个PRF三个发明者的缩写,但这个在实际中没有被使用,因为速度很慢,设想一下,使用Salsa发生器,现在来计算这个PRF在某个128位输入的值,我们必须运行Salsa发生器128次,然后就得到了一个PRF,但是其运行时间却是原版Salsa的128倍。
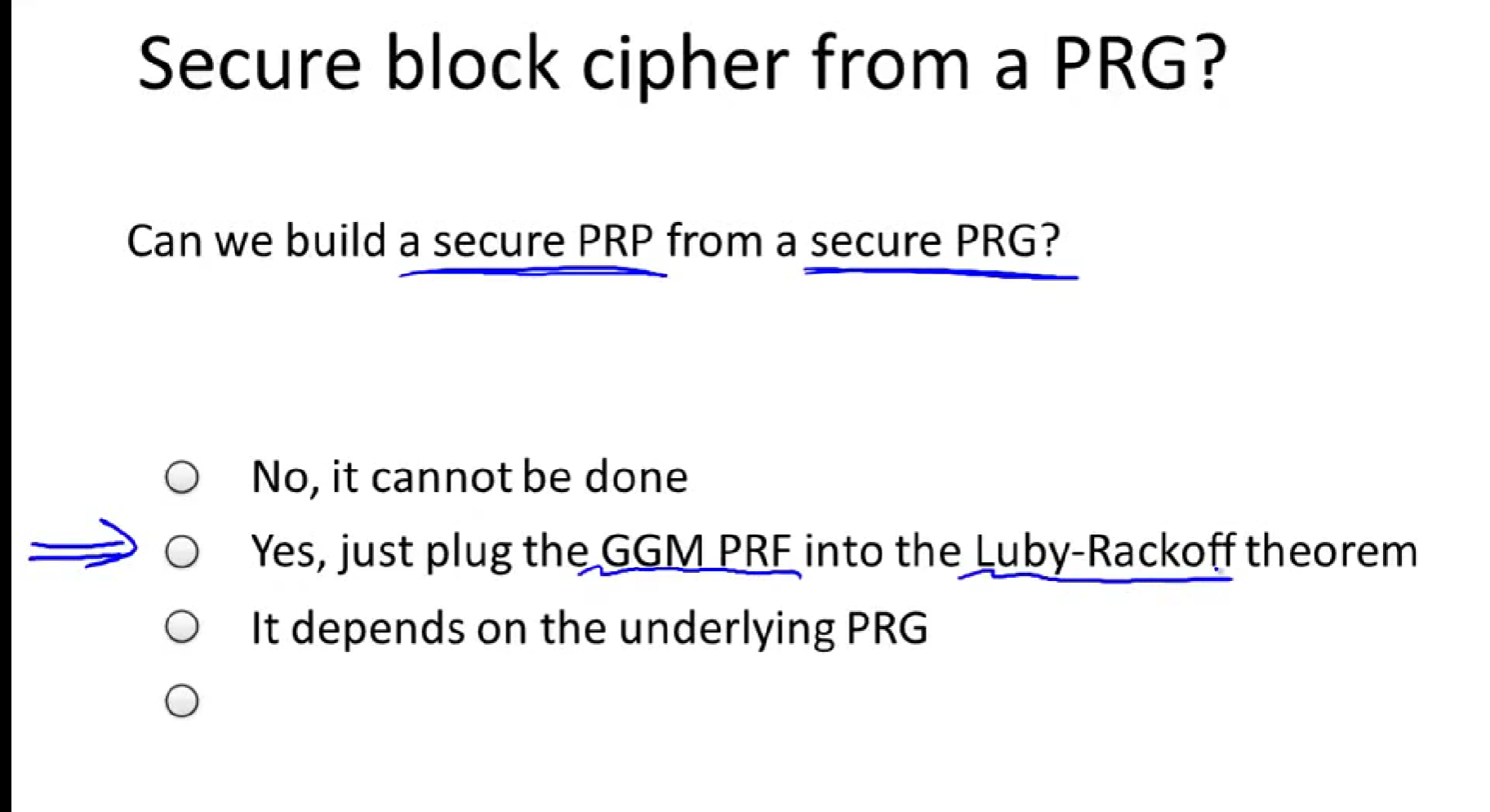
使用分组密码
Modes of operation: one time key

本节将使用分组密码来机密,并使用一次性的密钥。
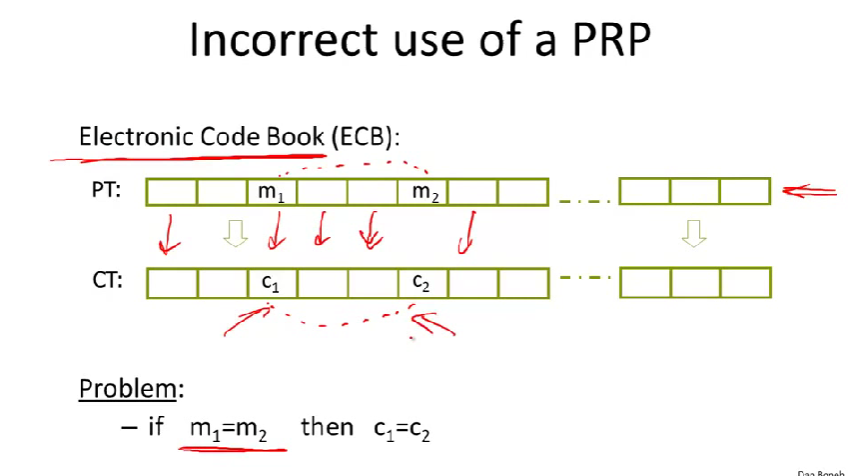
Electronic Code Book:电子密码本
将明文信息分成若干分组,每个分组大小与密码分组大小一样。 然后对每个分组单独加密,这种加密方式是不安全的,因为如果两个分组一样,那么他们的密文也一样。因此,攻击者可以学到关于明文的一些信息。

